Lineares Gleichungssystem zur Textaufgabe: Michael fährt um 15 Uhr mit seinem Fahrrad ...

Question

Michael fährt um 15 Uhr mit seinem Fahrrad von S über U in das 26 km entfernte Goch, wo er um 17 Uhr ankommt. Dort ist um 15.20 h Anne gestartet, und um 16 Uhr im 8 km entfernten U angekommen. Wann und wo haben sich beide getroffen?

Answer 1

eigentlich musst du deine amgaben doch nur in ein koordinatensystem einzeichen und dann den schnittpunkt als lösung nehmen:

Lösung: sie treffen sich um ca.: 16:20 ca. 16km von S entfernt.

warum ich das so gemacht habe?: wenn  michael um 15:00 uhr losfährt muss das kreuz auf 15:00 uhr und 0 km ,weil er ja noch nichts gefahren ist und wenmn er um 17:00 uhr 26 km weiter weg angekommen ist komtm das kreuz auf 17:00 uhr und 26 km.

Für anne muss man die zeichnung aber `rückwärts´ zeichnen weil sie ja von der entgegengesetzten richtung kommt und dann musst du dasselbe für anne auch einzeichnen wie für michael.

ich hoffe du verstehst meine antwort und kannst mit ihr etwas anfangen und deine frage ist geklärt!

Lilly

Comments

Hallo Lilly,

 

das ist verblüffend einfach zeichnerisch ermittelt. Gibt es auch eine rechnerische Lösung?

Geli

Answer 2

Ich habe hier noch eine weitere Möglichkeit, dazu braucht man aber zuerst die Geschwindigkeiten der beiden. Diese berechnet man aus Distanz durch Zeit:

s (Distanz) = 26 km

t_Michael (Zeit) = 2 h

v_Michael (Geschwindigkeit) = s/t_M= 26km/2h = 13km/h

 

s_Anne = 8 km

t_Anne = 40 min = 2/3 h

v_Anne = 8km / (2/3)h =12 km/h

 

Wichtig zu wissen ist hier, dass die Strecke SU = 18 km und UGoch = 8 km. 

Es gibt den Weg über eine Gleichung, ich benutze aber den einfachen Rechenweg mit der gemeinsamen Geschwindigkeit...

Wir haben hier dieses Situation:

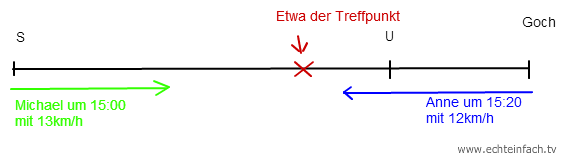
Nun muss man wissen, wieweit Michael in den 20 Minuten kommt, die Anne pausiert, nämlich:

t = 20 min = 1/3 h

v_M = 13 km/h

s = t*v = 13km/h* (1/3)h = 4.3333333 km

 

Diese zieht man der gesamten Strecke ab, dann rechnet man mit der gemeinsamen Geschwindigkeit, wie lange sie brauchen:

s_neu = s_tot - s_Michael = 26 km - 4.3333 km = 21.6666 km 

v_tot = v_A + v_M = 25 km/h

t_Zusammen = s/t = 0.866666 h = 52 min

 

Damit kann man ausrechnen, wie weit der Treffpunkt von Gauch entfernt ist:

t_Z = 0.86666 h

v_A = 12 km/h

s_A = 10.4 km

Dies sind die Lösungen...

Lösungssatz: Der Treffpunkt liegt 10.4 km von Gauch entfernt und sie treffen sich um 16:12 Uhr (Dies ergibt sich aus 15:20+52 min)

 

Ich hoffe, ich konnte helfen und du verstehst es jetzt!

Simon

Comments

Also, Aufgabe lautet: Anne kommt um 16:00 Uhr in U an.

Offensichtlich fährt die nicht weiter. Die beiden treffen sich also in U.

Jetzt ist nur noch fraglich, wie lange Michael bis U benötigt.

Von X nach U sind es 18 km. Er fährt mit 13 km/h, benötigt also
18/13 Stunden, also rd. 83 Minuten.

Ausgehend von 15:00 Uhr treffen sich beide also in U um ca. 16:23 Uhr.