Extremwerte bei quadratischen Termen

Question

Hey :) 

Ich habe in zwei Wochen meine Nachprüfung in Mathe und wiederhole gerade nochmal alle Themen die wir in dem letzten Schuljahr durchgekommen haben. Jetzt bin ich gerade bei dem Thema "quadratische Terme". Und Ehrlich gesagterweise kann ich mit diesem Thema gar nichts anfangen. Ich weiß höchstens nur noch, dass dieses Thema etwas mit den GTR (Grafischen Taschenrechner) zu tun hat.. Aber sonst hab ich keinen Plan. Wie Zum Beispiel bestimmt man einen Extremwert? Wie bestimmt man das Minimum bzw. Das Maximum? 

Answer 1

Die allgemeine Form des quadratischen Termes lautet

ax^2 + bx + c

Wenn du davon jetzt die Nullstellen wissen möchtest, kannst du die abc-Formel nehmen

x = (-b ± √(b^2 - 4ac))/(2a)

Diese Formel ist ganz nützlich, denn nimmst du den Wurzelterm weg, bleibt die x-Koordinate vom Scheitelpunkt übrig.

Sx = -b/(2a)

Die y-Koordinate vom Scheitelpunkt erhält man jetzt durch einsetzen in die allgemeine quadratische Form.

Mehr braucht man dann fast auch schon nicht mehr wissen.

Answer 2

Am GTR habt ihr sicher Parabeln angeschaut und den Scheitelpunkt der Parabeln bestimmt.

Da kann man die Parabelgleichung durch quadratische Ergänzung in Scheitelpunktform bringen. 

Hierzu schaust du am besten mal folgendes Video: https://www.matheretter.de/wiki/quadratische-funktionen

Man kann aber oft auch über die Nullstellen gehen (pq-Formel oder abc-Formel benutzen), da der Scheitelpunkt immer in der genau in der Mitte zwischen den beiden Nullstellen der Parabel liegt.

Etwas Einführendes zu quadratischen Gleichungen hier: https://www.matheretter.de/wiki/quadratischegleichung

Answer 3

Hallo Annapanda,

wenn Du eine quadratische Funktion der Form
f(x) = ax² + bx + c
hast,
kannst Du zur Bestimmung der Extremwerte auch die erste und zweite Ableitung bilden:
f'(x) = 2ax + b
f''(x) = 2a

Die erste Ableitung, also f'(x) setzt Du = 0 und erhältst so einen "Kandidaten" für ein Extremum (notwendige Bedingung). Wenn Du das gefundene x dann in f''(x) einsetzt und der Wert der Ableitung < 0 ist, hast Du an dieser Stelle ein Maximum, wenn er > 0 ist, hast Du an dieser Stelle ein Minimum.
Dann den x-Wert noch in f(x) einsetzen, um die entsprechende y-Koordinate herauszufinden.

Beispiel:
f(x) = 3x² - 6x - 5
f'(x) = 6x - 6
f''(x) = 6

f'(x) = 6x - 6 = 0 | x = 1
f''(1) = 6 > 0 | Minimum an der Stelle x = 1
f(1) = 3 - 6 - 5 = -8 | y = -8
Minimum der Funktion im Punkt (1|-8)

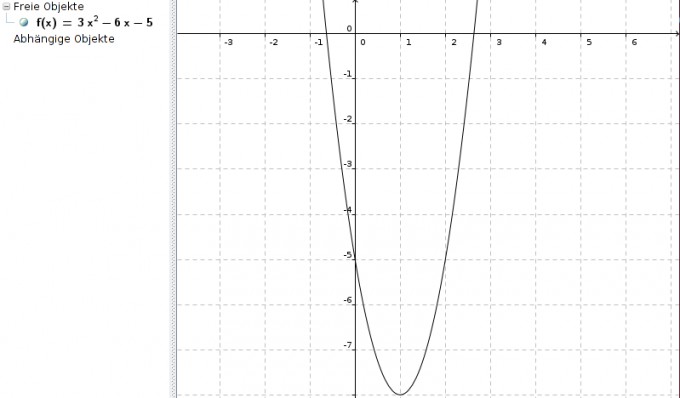
Wahrscheinlich ist die andere Vorgehensweise (Verwendung der Scheitelpunktform) aber schneller und einfacher :-)

Besten Gruß