Lage einer Geraden gegenüber Parabel

Question

Gegeben seien die Funktionen f(x) = 1/2x² - 4x + 14 und g(x) = 2x + 4

Untersuchen Sie, welche Lage die Gerade g relativ zur Parabel f einnimmt. Bestimmen Sie ggf. die Schnittpunkte.

Danke schon mal für die Hilfe

Answer 1

um die Schnittpunkte zu bestimmen setze man

f(x) =g(x)

1/2x²-4x+14=2x+4           | -2x -4

1/2 x²-6x +10=0              | *2

      x²-12x +20=0             | faktorisieren

(x-10)*(x-2)=0              L={10,2}

in f(x) und g(x) einsetzen

f(10) = 24          f(2) =8

g(10)= 24           g(2)=8

Schnittpunkte  sind   S (10|24) und  P(2|8)

Answer 2

Man tut so, als würde man die Schnittstellen der beiden Graphen berechnen, kann aber aufhören sobald man weiss wieviele Lösungen die Gleichung hat.

f(x) = 1/2 x² - 4x + 14 und g(x) = 2x + 4

Gleichsetzen

1/2 x² - 4x + 14 = 2x + 4          |-2x - 4

1/2 x^2  - 6x + 10 = 0           |*2

x^2 - 12x + 20 = 0

x_1,2 = 1/2 * (12 ± √(144 - 80))

=  1/2 * (12 ± √64)

64>0 daher 2 Lösungen.

D.h. die Gerade schneidet die Parabel in 2 Punkten.

Kontrolle: Graphen:

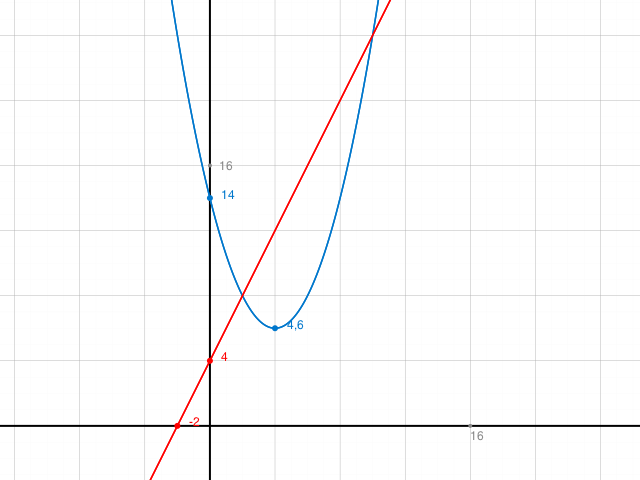
Nachtrag: Weitere Fälle

Stünde unter der Wurzel 0: Eine Lösung. Gerade würde Parabel berühren.

Stünde unter der Wurzel eine negative Zahl: Keine Lösung. Gerade und Parabel hätten keinen gemeinsamen Punkt. Gerade verliefe neben der Parabel.

 

Comments

Die Schnittpunkte hat Akelei schon berechnet.