G(x) = - 1.3·x^3 + 150·x^2 - 30000
a) bestimme den bereich der stückzahlen mit positivem gewinn
Nullstellen G(x) = 0
-1.3·x^3 + 150·x^2 - 30000 = 0
Da ich keine ganzzahligen Lösungen finde benutze ich das Newtonverfahren und finde Nullstellen bei
x = 113.5962769 ∨ x = -13.38687154 ∨ x = 15.17520995
Bei einer Funktion 3. Grades mit negativem Leitkoeffizient ist der positive Bereich 16 ≤ x ≤ 113.
b) bei welcher stückzahl ist der gewinn am größten?
Extremstellen G'(x) = 0
300·x - 3.9·x^2 = 0
Lösung mit abc-Formel ist bei
x = 76.92307692 ∨ x = 0
Bei 77 Stück ist der Gewinn am größten.
c) für welche stückzahlen beträgt der gewinn etwa 200 000 euro?
G(x) = 200000
- 1.3·x^3 + 150·x^2 - 30000 = 200000
Das Newtonverfahren liefert die Lösungen
x = 53.44519659 ∨ x = -34.37160459 ∨ x = 96.31102338
Also bei 53 und 96 Stück liegt der Gewinn bei etwa 200000 Euro.
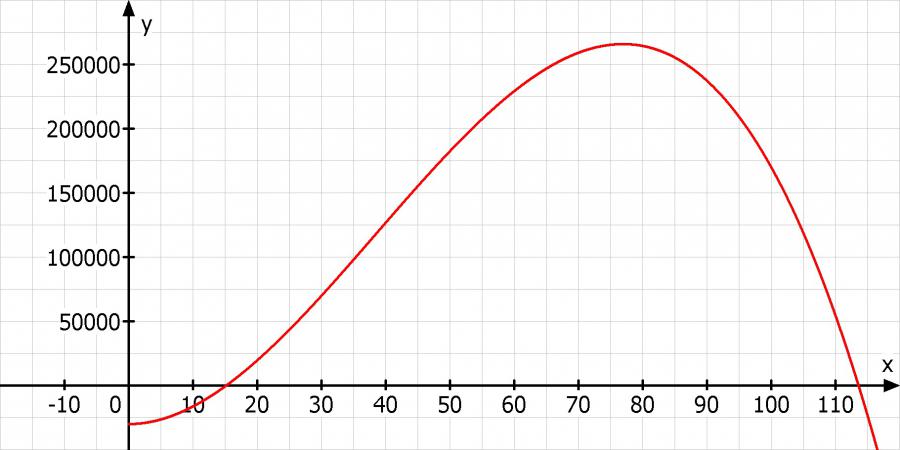
Skizze: