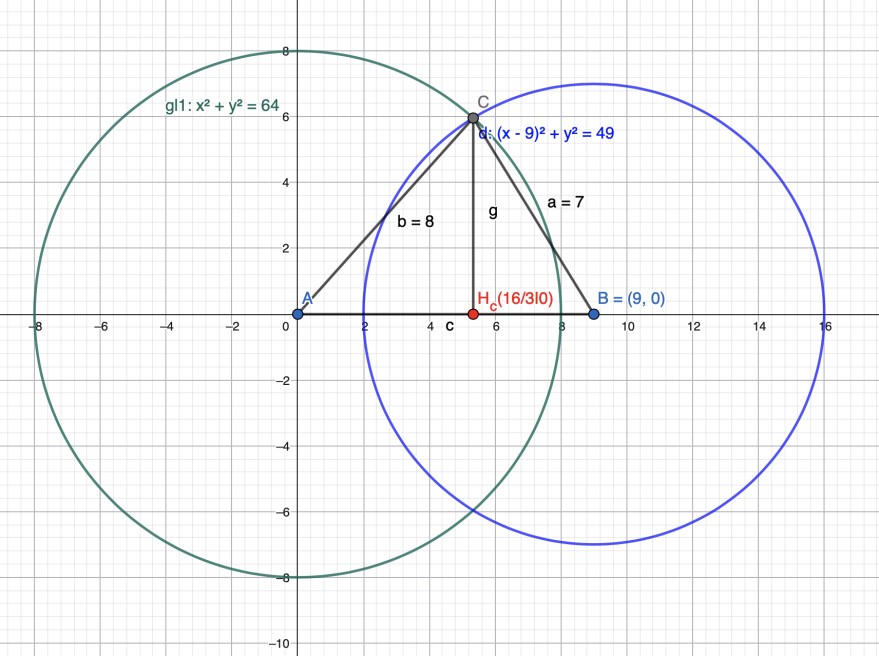
Planfigur:
(2)
Kreis um A(0|0) mit r=8:
\(x^2+y^2=64\) → \(y^2=64-x^2\)
Kreis um B(9|0) mit r=7:
\((x-9)^2+y^2=49\) → \((x-9)^2+64-x^2=49\)
\(x^2-18x+81+64-x^2=49\) →\(18x=96\)→\(x=\frac{16}{3}\)
\( \cos(α)=\frac{16}{8\cdot3}=\frac{2}{3}\).
\( α≈48,1896°\)
Berechnung von β:
\( \cos (β)=\frac{9-\frac{16}{3}}{7}=\frac{11}{21}\)
\(β≈58,412°\)
Berechnung von γ: Über die Winkelsumme im Dreieck