Parabel im dreidimensionalen Koordinatensystem

Question

wie konstruiere ich eine Parabel im dreidimensionalen Koordinatensystem?

Ich habe 25 Punkte P1 - P25  (x/y/z), mir würde es reichen, wenn ich aus 5 (habe gehört, dass man aus 5 Punkten eine Parabel konstruieren kann) ein Parabel konstruiere. Z.B. eine Parabel aus P1, P7, P13, P19,P24 erstellen und dann die Strecke von P1 bis P24 berechnen

Einfach die Strecke vom P1 bis P5 ist mir zu ungenau, da sie gerade ist.

 

Schon mal vielen Dank

Comments

Wie meinst du das genau? Eine Parabel ist ja eine ebene Kurve 2. Grades. Da müsstest du erst mal wissen, ob all deine 5 Punkte in derselben Ebene im Raum liegen.

---

Hier ist eine Arbeit zu Parabeln im Raum, vielleicht kann das weiterhelfen.

http://elib.mi.sanu.ac.rs/files/journals/tm/10/tm614.pdf

Answer 1

Wenn ich das richtig versteht, kannst du das z.B. über qti-Plot machen:

Du erstellst eine Matrix, änderst die Dimensionen der Matrix mit einem Rechtsklick und der Auswahl von "Dimension festlegen..." und fügst dann die Funktionswerte an.

Über die Schaltfläche "3D-Diagramm" kannst du dann einen von mehreren Diagramm-Stilen auswählen.
Das sieht dann z.B. so aus:

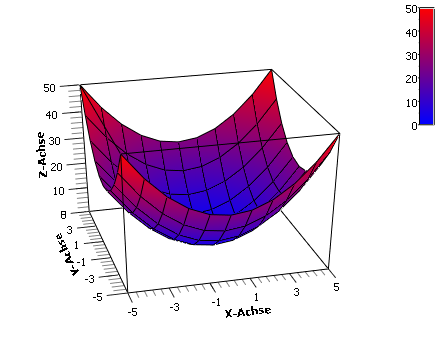
Falls du tatsächlich eine Formel für die Parabel haben möchtest, könntest du zum Beispiel gemäß

r² = x²+y²

eine vereinfachte Koordinate einführen und dann (ebenfalls mit qti-Plot) einen linearen Fit der Form z = a*(r-c)² + d durchführen.

Um eine Parabel eindeutig festzulegen reichen übrigens eigentlich 3 Punkte, allerdings ist es sinnvoller, eine Regression durchzuführen, die versucht, eine Parabel zu finden, die alle Punkte möglichst gut annähert.