Gleichschenkliges Dreieck, formale Herleitung von a(x) = 0.5√(L)√(Lx^2 - 4x^3)

Question

Wir müssen herleiten, dass für L(2x+2b) folgende Beziehung gilt:

a) Beweise für die Dreiecksfläche A die Beziehung

\( A(x)=\frac{\sqrt{L}}{2} \sqrt{L x^{2}-4 x^{3}} \)

Das Dreieck sieht so aus:




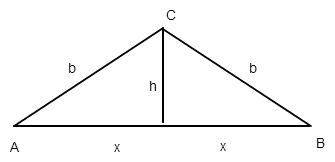
Wie beginnt man solch eine Aufgabe am besten?

PS: L(2x+2b) ← Ich glaube, dass damit der Umfang gemeint ist. Also alle Seiten addiert ergibt L.

Answer 1

wenn du bei A(x) für L=2x+2b einsetzt und umformst bekommst
du  x*wurzel aus(b^2 - x^2) heraus
und das ist tatsächlich der Flächeninhalt, denn mit A= 2x*h/2 = x*h
und h mit Pythagoras wurzel aus (b^2-x^2) stimmt es überein