Deine Kostenfunktion macht so wie sie gegeben ist keinen Sinn. Der Koeffizient vor der höchsten Potenz (7) ist negativ. Damit haben wir bei einer sehr hochen Produktion (x gegen unendlich) negative Kosten. Das darf nicht sein.
E(x) = 504·x
K(x) = 1.5·x^3 - 30·x^7 - 30·x^2 + 450·x + 600
G(x) = E(x) - K(x) = 504·x - (1.5·x^3 - 30·x^7 - 30·x^2 + 450·x + 600) = 30·x^7 - 1.5·x^3 + 30·x^2 + 54·x - 600
b) Zeigen sie,dass bei 4 ME Erlös und Kosten gleich sind.
Wenn Kosten und Erlös gleich ist sollte der Gewinn Null sein.
G(4) = 491520
Also haben wir bei 4ME keinen Gewinn von Null und damit sind hier Kosten und Erlös nicht gleich. Auch das deutet auf eine verkehrte Kostenfunktion hin.
Ich nehme also mal die Kostenfunktion mit
K(x) = 1.5·x^3 - 30·x^2 + 450·x + 600
an, wie sie mehr Sinn macht
G(x) = E(x) - K(x) = 504·x - (1.5·x^3 - 30·x^2 + 450·x + 600) = - 1.5·x^3 + 30·x^2 + 54·x - 600
G(4) = 0
Hier ist jetzt also auch der Gewinn gleich Null wie vermutet.
c) Gewinnschwelle und Grenze sind die Nullstellen der Gewinnfunktion G(x) = 0
- 1.5·x^3 + 30·x^2 + 54·x - 600 = 0
Mit 4 als eine Lösung Polynomdivision und abc-Lösungsformel komme ich auf die Nullstellen
x = 8 - 2·√41 ∨ x = 2·√41 + 8 ∨ x = 4
x = 20.80624847 ∨ x = -4.806248474 ∨ x = 4
Die Gewinnschwelle liegt also bei 4 und die Gewinngrenze bei 20.81 ME
K(4) und K(20.81) kannst du sicher selber berechnen.
d) Berechnen sie, bei welcher Produktionsmenge der Gewinn maximal wird und berechnen sie die höhe des maximalen gewinn
Gewinnmaximum bei G'(x) = 0
G'(x) = - 4.5·x^2 + 60·x + 54 = 0
Mit der abc-Formel ergibt sich die Lösung
x = 20/3 - 2·√127/3 ∨ x = 2·√127/3 + 20/3
x = -0.8462851130 ∨ x = 14.17961844
Wir haben das Gewinnmaximum bei 14.18 ME
Die Gewinnhöhe beträgt hier G(14.18) bitte auch selber ausrechnen.
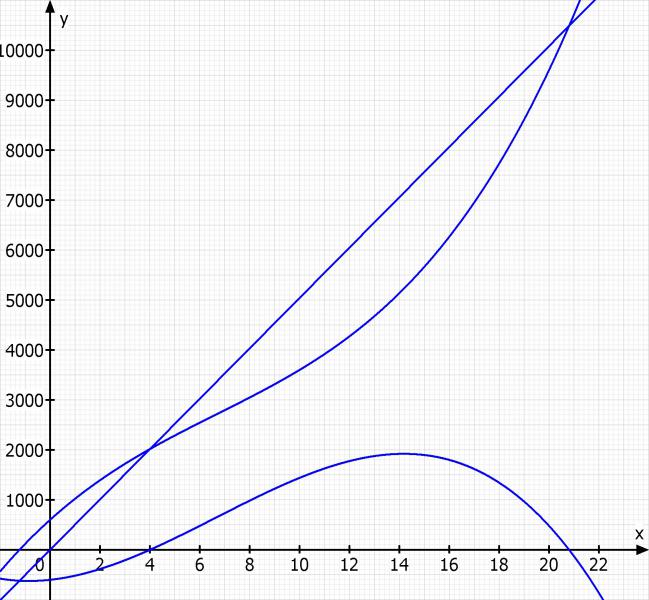
Hier noch eine Skizze