Ist die Funktion so richtig? Weil bei einer Funktion 3. Grades gibt es ja nur einen Wendepunkt und eine Wendetangente und nicht mehrere.
f(x) = x^3 - 6x^2 + 15x + 32
f'(x) = 3·x^2 - 12·x + 15
f''(x) = 6·x - 12
Wendepunkt bei f''(x) = 0
6x - 12 = 0
6x = 12
x = 2
f(2) = 46 (y-Koordinate des Wendepunktes)
f'(2) = 3 (Steigung im Wendepunkt)
Damit kann ich die Funktion der Wendetangente in der Punkt-Steigungs-Form aufstellen.
t(x) = 3*(x - 2) + 46 = 3x + 40
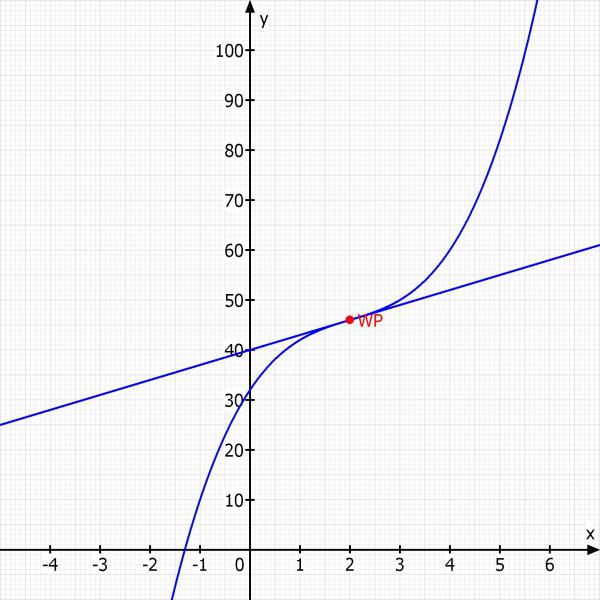
Skizze