Aus unserem Wissen, und meiner Vermutung : 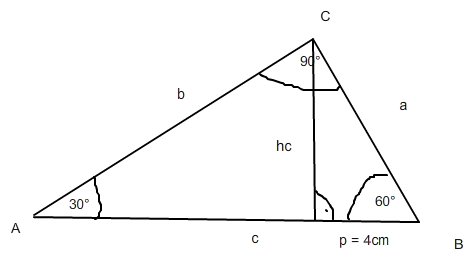
Wir schauen uns das kleinere Dreieck rechts an.
Unser Ziel ist Seite a.
cos(60°) = p/a
Da wir p haben stellen wir mal um !
cos(60°)*a = p | : cos(60°)
a = p/cos(60) = 8cm.
Diese Seite hätten wir schon mal !
Da im Dreieck alle Innenwinkel addiert 180° ergeben müssen, können wir sagen, dass gamma in 60° und 30° geteilt wurde ( 90°-60° = 30° V 90°-30° = 60°)
Wir berechnen nun die Höhe hc.
Aber jetzt der sinus !
sin(60°) = hc / a
sin(60)* a = hc = 6,92 cm
Damit kann man viel machen !
Wir rechnen als nächstes b aus.
cos(60°) = hc/b
cos(60) * b = hc
b = hc/cos(60) = 13,85cm
Nun zu dem Teilabschnitt von c !
tan(60) = c' / hc
c' = tan(60) * hc = 11,98 cm
Nun noch die 4 cm von p addieren.
--> c = 15,98 cm
Probe mit Pythagoras :
a² + b² = c²
8² + 13,85² = c²
c=√255,8cm = 15,99 cm
Stimmt also fast komplett überein !
Nun die Lösung
U = a + b + c = 37,844 cm
Gruß Luis