Nullstelle bei Funktion 4 Grades

Question

Ich versuche die Nullstellen bei einer Funktion 4 Grades auszurechnen.

f(x)=1/9(-x^4+8x^3-18x^2+36)

Ich glaube, dass 1/9 eine Nullstelle ist

Kann man eigentlich bei einer Funktion 4 Grades auch mit dem Hornerschema arbeiten oder geht das nur bei Funktionen 3 Grades?

Comments

Woher hast du diese Funktion?

Die Funktion hat keine Nullstellen, die man erraten könnte. Vgl. https://www.wolframalpha.com/input/?i=-x%5E4%2B8x%5E3-18x%5E2%2B36

-x^4+8x^3-18x^2+36

1/9 hat nichts mit der Nullstelle zu tun. Du kannst den Faktor 1/9 bei der Nullstellensuche sogar ignorieren.

Answer 1

Klar Hornerschema geht bei allen Polynomen, wird halt jedes Mal der
Grad um kleiner, also hier von 4 auf 3 dann von 3 auf 2 und dann pq-Formel oder so.

Aber bei dieser Aufgabe ist das Problem, dass keine Lösung zu raten ist.
Ich vermute, dass hinter der 36 noch ein x kommt.
Dann kannst du erst einmal x ausklammern und bei dem Rest kannst du x=6 raten
und machst dann Horner.  Der quadratische Term hat dann keine Nullstellen mehr,
also gibt es nur 0 und 6.

Answer 2

1/9 ist definitiv keine Nullstelle.

Horner-Schema kannst du natürlich auch für Funktionen 4. Grades (sogar für beliebigen Grad) versuchen, ob es zum Ziel führt ist natürlich eine andere Frage.

Hier geht's wahrscheinlich aber nur durch Approximation (ohne es selbst gerechnet zu haben).

Gruß

Answer 3

1/9*(-x^4+8x^3-18x^2+36)=0 | *(-9)

0=x^4-8x^3+18x^2-36 

Kein Mathe Lehrer unterhalb Klasse 12 stellt Fragen, wo derart "krumme" (irrationale) Ergebnisse herauskommen.  

Also entweder hast Du Dich (oder er sich) verschrieben, oder es sollen wirklich höhere Algorithmen angewendet werden.

Man könnte das Newton-Näherungsverfahren anwenden (siehe Wikipedia) ...  

Aber viele wissen nicht, dass es analog zum quadratischen Polynom -> pq-Formel auch bei den Polynomen von Grad 3 und 4 exakte explizite Lösungsformeln gibt,

die leider kein Lehrer lehrt (oder wenigstens anspricht): Cardanische Formeln oder gleich die explizite PQRSTUVW -Formel

siehe http://www.lamprechts.de/gerd/php/gleichung-6-grades.php  

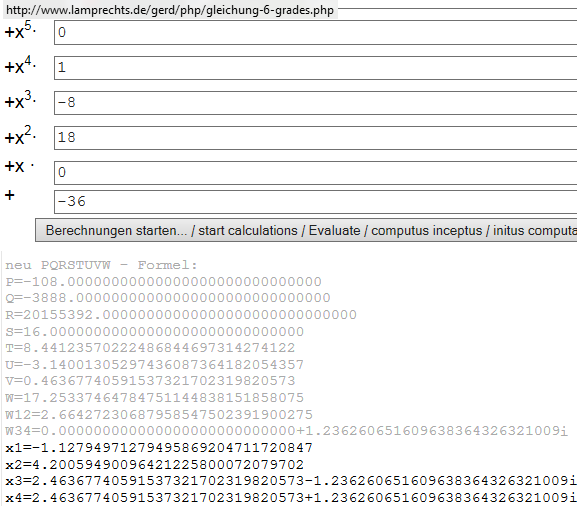
Wenn Du mehr Nachkommastellen oder das Ergebnis in Wurzelschreibweise benötigst (etwa 1 Seite voller verschachtelter Kubischer Wurzeln ) benötigst, melde Dich.

Answer 4

Da sich nach Probieren keine ganzzahlige Lösung findet (Teiler des absoluten Gliedes), sucht man mit Hilfe einer Wertetabelle zwei benachbarte im Vorzeichen unterschiedliche Werte, zwischen denen dann die genaue Lösung z. B. mit den Newtonverfahren gefunden werden kann.