Berechne Abstand zwischen Raumdiagonale und Punkt - Winkel, Raumdiagonale und Fläche im Quader

Question

Quader:

1. Wie weit ist C´von dieser Raumdiagonale (=d) entfernt?

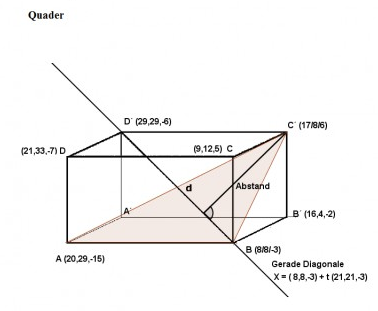
Berechnung:

Betrag Kreuzprodukt der Ebene BD´und BC´dividiert durch Betrag Richtungsvektor der Geraden.

bd´= (21,21,-3)  :  3   =  (7,7,-1)

bc´ = (9,0,9)

Kreuzprodukt:   (63, -72, -63)
   
Abstand d = Betrag Kreuzprodukt / Betrag Richtungsvektor Gerade    =  11,51

oder:  d (P, g) =    |AP x g₀.|  = ~ 11,46

Frage: Kann man das nicht anders, einfacher, logischer berechnen. Ich verstehe diese Formeln nicht – was wird da gemacht ?

2) In welchem Winkel trifft die Raumdiagonale die Fläche ABC´?

Ist das der Winkel zwischen Normalvektor der Ebene ABC´ und Richtungsvektor der Diagonalen oder Winkel, wo Raumdiagonale die Ebene ABC`schneidet oder läuft es ganz anders.

Answer 1

Frage: Kann man das nicht anders, einfacher, logischer berechnen; 
Du kannst die Koordinatengelichung der Normalenebene zu g durch C' bestimmen und diese dann mit g schneiden.
Ansatz: E: 21x + 21y - 3z = d
Oder einfacher, wenn der Richtungsvektor mit 3 gekürzt wird:
Ansatz E: 7x + 7y - z=d.
Nun C einsetzen, d bestimmen.

Dann Gerade mit Ebene schneiden → S

Zum Schluss Abstand SC ausrechnen.

Das gibt aber mehr zu rechnen.

2) In welchem Winkel trifft die Raumdiagonale die Fläche ABC´? 
Ist das der Winkel zwischen Normalvektor der Ebene ABC´ und Richtungsvektor der Diagonalen 
oder 
Winkel, wo Raumdiagonale die Ebene ABC`schneidet?

Die Ebene ABC' enthält auch den Punkt D' und deshalb die Raumdiagonale g.
Folglich ist der gesuchte Winkel 0.

Du kannst dir das so überlegen:
Ebenen schneiden gegebene parallele Ebenen immer in Parallelen.
Also müssen bei Ebenen im Quader die entsprechenden 'Spuren' in den Seitenebenen zueinander parallel sein.
Konkret ist AD' in der Ebene, weil BC' in der Ebene liegt. Ebenso D'C', weil AB in der Ebene liegt.
Nun siehst du, dass die Raumdiagonale BD' auch in dieser Ebene liegt.

 

Comments

Vielen Dank für die Erklärungen

- es ist wirklich sehr viel zu rechnen - besser doch diese Formel - jetzt weiß ich, was dahinter steckt.

- Die Fläche ABC´ist dann als Ebene anzusehen, die ich mit Bleistift über den gesamten Quader zeichen kann - dann liegt die Diagonale eigentlich auf/in der Ebene und der Winkel ist Null.