Viereck wird von Geraden begrenzt

Question

Frage:

Wie berechnet man den Flächeninhalt eines Vierecks, das von vier Geraden als Gleichungen (in diesem Fall \( x=-3, \quad x=5, \quad y=-\frac{1}{2} x+\frac{7}{2} \quad \) und \( \quad y=\frac{1}{8} x-\frac{25}{8} \)) begrenzt wird, aus?

Meine Ideen:

Ich würde erstmal versuchen, die Gleichungen auszurechnen, indem ich die erste und die zweite Gleichung je einmal in die dritte und einmal in die vierte einsetze. Aber was dann?

Answer 1

Zeichne das doch einfach mal:

Das Viereck ist ein Trapez und lässt sich recht einfach berechnen:

A = 1/2 * (8.5 + 3.5) * 8 = 48

Answer 2

Hi,

erst mal in ein Schaubild übertragen, damit wir eine Vorstellung haben:

 

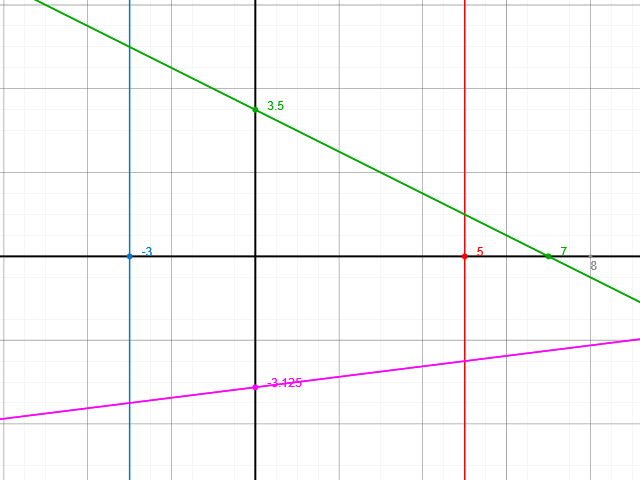
Nun gilt noch zu wissen, dass sich der Flächeninhalt eines allgemeinen Vierecks zu

A=1/2*e*f*sin(α) ergibt.

e und f sind dabei die Diagonalen und α deren Schnittwinkel.

 

Bestimmen der Diagonalen e:

Schnittpunkt mit blau-grün und rosa-rot

blau-grün:

y=-0,5x+3,5 bei x=-3 -> y=1,5+3,5=5

S₁=(-3|5)

rosa-rot:

y=1/8x-25/8 bei x=5 -> y=5/8-25/8=-20/8=-2,5

S₂=(5|-2,5)

 

Die für uns interessante Länge e, ist also durch die Punkte S₁ und S₂ gegeben.

Die Länge ergibt sich mittels Pythagoras: e^2=(5-(-3))^2+(-2,5-5)^2=120,25

e=√120,25

 

Das gleiche nun mit der Diagonalen f.

Schnittpunkt mit rosa-blau und grün-rot

rosa-blau:

y=1/8*x-25/8 bei x=-3: y=-3,5

S₃=(-3|-3,5)

grün-rot:

y=-0,5x+3,5 bei x=5: y=1

S₄=(5|1)

 

Die für uns interessante Länge f, ist also durch die Punkte S₃ und S₄ gegeben.

Die Länge ergibt sich mittels Pythagoras: f^2=(5-(-3))^2+(1-(-3,5))^2=84,25

f=√84,25

 

Verbleibt noch die Bestimmung des Winkels α:

m_e=(-2,5-5)/(5-(-3))=-15/16

m_f=(1-(-3,5))/(5-(-3))=9/16

 

tan(α)=|(m_e-m_f)/(1+m_em_f)|=|-384/121|=384/121

 

α=72,51°

 

Damit ist der Flächeninhalt

A=48 FE

 

 

Hoffe ich hab mich nicht verrechnet. Hoffe außerdem das Prinzip ist verstanden.

 

Grüße

(P.S.: Falls was offen ist -> ich bin essen ;))