Aufgabe:
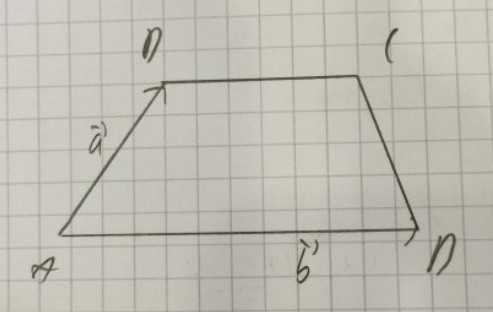
Im abgebildeten Trapez ist die Seite \( \overline{\mathrm{CD}} \) halb so lang wie die Seite \( \overline{\mathrm{AB}} \). In welchem Verhältnis teilt der Schnittpunkt S die Diagonalen \( \overline{\mathrm{DB}} \) und \( \overline{\mathrm{AC}} \) ?
a) Stelle die Vektoren \( \overline{\mathrm{AS}} \) und \( \overline{\mathrm{DS}} \) als Linearkombination von \( \overline{\mathrm{AD}} \) und \( \overline{\mathrm{AB}} \) dar.
b) Nutze die Tatsache aus, dass \( \overline{\mathrm{AD}}+\overline{\mathrm{DS}}+\overline{\mathrm{SA}}=0 \) gilt und bestimme das Teilungsverhältnis.
Abbildung: