Skalarproduktvektorräume über die Komplexen Zahlen

Question

Es soll überprüft werden ob folgender Vektorraum über ℂ mit der angegebenen Sesquilinearform zum Skalarproduktraum wird.

ℂ^3x1 über ℂ mit

$$<x,y> = \bar{x}^{tr} * \begin{pmatrix} 2 & -i & -2 \\ i & 2 & -i \\ 2 & i &2 \end{pmatrix} *y$$

für x,y ∈ ℂ^3x1

Ich habe zunächst versucht ein $$x=(x_1,x_2,x_3)$$ zu finden und die pos. definitheit zu widerlegen..

= 

= 

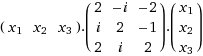
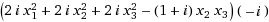
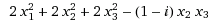
bedeutet es hier dass die pos. definitheit stets erfüllt ist?

Comments

Update:

wenn ich x=(-i,0,0) wähle.. komme ich auf einen Wert <0. Reicht das die pos. definitheit zu widerlegen?

= -2

---

Sicher, dass die Matrix korrekt dargestellt ist?

---

Stimmt, in der 2ten Zeile/ 3te Spalte sollte ein -i statt -1 stehen:

Dann wär das Ergebnis= 2 (x_(1)²+x_(2)²+x_(3)²)

aber auch hier sollte mein Bsp. mit x= (-i,0,0) zum Widerspruch führen oder nicht?

---

Sollte für diese Matrix nicht $M^\mathsf T=\overline M$ gelten?
Außerdem solltest du von links mit dem konjugiert komplexen Zeilenvektor $\overline x^\mathsf T$ multiplizieren.

Answer 1

ist nicht erfüllt, weil <x,x> noch nicht mal immer reell ist, also erst recht nicht ≥ 0.