trigonometrische Interpolation und schnelle Fouriertransformation

Question

Guten Morgen , kann mir jemand die beiden oben genannten Dinge der numerischen Mathematik erklären? Ich verstehe es leider auf Wikipedia etc nicht ..

Comments

Ich denke da musst Du schon etwas genauer sagen, was Du nicht verstehst. Ich kann ja nicht eine ganze Abhandlung aus einem Buch abschreiben. Wofür man die trigonometrische Interpolation benutzt, steht doch gut erklärt in Wikipedia.

---

Wie ich da etwas ausrechne . Ich verstehe den Algorithmus einfach nicht und soll damit am Mittwoch In einer Klausur was berechnen aber verstehe es leider gar nicht .

---

Wenn es in der Klausur vorkommt hast du doch bestimmt irgendwelche Übungsaufgaben, die in diese Richtung gehen. Versuch doch diese zu posten und zu schreiben wo deine Probleme sind?

---

Das sind die einzigen zwei Aufgaben in diese Richtung und die hab ich null hinbekommen und konnte leider auch nicht zur Korrektur , da zeitgleich schon die erste Klausur des Semesters war .

Answer 1

die erste Aufgabe ist hier gelöst auf Folie 5 und 6

https://www.google.de/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&sqi=2…

Aufgabe 2:

Schreib doch mal hin, wie Dein allg. trigonometrisches Polynom aussieht, danach können wir dann die Koeffizienten bestimmen.

Comments

Genau das versteh ich ja nicht wie das aussehen soll , da ich im Internet immer wieder was neues finde . Aber schonmal Danke für die Lösung

---

Was verstehst Du nicht, die Lösung von Aufgabe 1 oder weisst Du gar nicht wie ein trigonometrisches Polynom aussieht?

---

Hi,
gesucht ist ein Polynom der Form $$p(x) = \frac{\alpha_0}{2} + \sum_{k=1}^n \left[ \alpha_k \cos(kx) + \beta_k \sin(kx) \right]$$
Die Koeffizienten berechnen sich nach
$$(1) \quad \alpha_k = \frac{2}{m} \sum_{j=0}^{m-1} f_j \cos(k x_j)$$ und
$$(2) \quad \beta_k = \frac{2}{m} \sum_{j=0}^{m-1} f_j \sin(k x_j)$$
mit $x_j = \frac{2\pi j}{m}$ sowie $f_j = f\left(x_j\right)$
Für $m$ gilt, ist $m = 2n$ ist $\beta_n = 0$ und $\alpha_n$ muss halbiert werden.

Für Deinen speziellen Fall betrachte die Funktion $f(x) = |x-\pi|$, also die um $\pi$ nach rechts verschobene Betragsfunktion und führe obige Berechnungen aus. Das approximierende Polynom ist dann $p(x+\pi)$, also die wieder nach links geschobene Betragsfunktion.

Für $n=3$ sieht das z.B. so aus

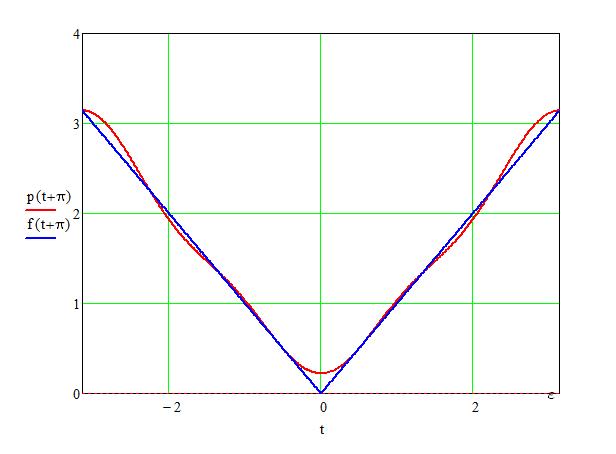
Um  die geforderte Genauigkeit zu erreichen habe ich 101 Koeffizienten benötigt. Die größste Ungenauigkeit tritt bei $t = 0$ auf.