Hallo
Ich schreib Dir mal auf, welche Ergebnisse ich herausbekommen habe.
a) Wie hoch steht das Wasser 10 Minuten nach Füllbeginn?
h(t=10) = 20*t^{1/3} = 20*10^{1/3} = 43,09;
A.: Das Wasser erreicht eine Füllhöhe von ca. 43 cm.
b) Wann ist der Behälter voll?
h(t) = 100;
20*t^{1/3} = 100;
t^{1/3}=5;
Um die Gleichung nach t aufzulösen braucht man die Umkehrfunktion, man muss also beide Seiten hoch drei setzen.
t = 5^3 = 125;
A.: Der Behälter ist nach 125 min gefüllt.
c) Wie schnell steigt der Wasserstand 10 Minuten nach Füllbeginn?
Um die Geschwindigkeit zu einem bestimmten Zeitpunkt zu berechnen braucht man die erste Ableitung.
h'(t) = 20/3*t^{-2/3};
h'(t=10) = 20/3*10^{-2/3} = 1,44;
A.: Zum Zeitpunkt t = 10 min steigt das Wasser mit einer Geschwindigkeit von 1,44 cm/min.
d) Wann steigt das Wasser mit einer Geschwindigkeit von 1cm/min?
Nun muss gelten h'(t) = 1;
20/3*t^{-2/3} = 1;
t^{-2/3} = 3/20;
Jetzt zu der Umformung, die Dir Schwierigkeiten bereitet. Zunächst einmal schreibe ich t^{-2/3} um:
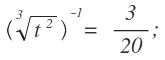
Wenn Du das auflösen möchtest muss Du die Umkehrfunktionen anwenden. Der Übersicht wegen mache ich das der Reihe nach und beginne mit der äußeren Funktion.
Hoch minus 1 kehrt man um indem man entweder beide Seiten hoch minus 1 setzt oder den Kehrbruch bildet, was auf das Gleiche hinausläuft:
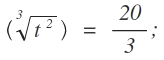
Nun muss die Kubikwurzel aufgelöst werden. Dazu werden beide Seiten hoch 3 gesetzt:
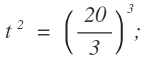
Jetzt noch das Quadrat auflösen. Dazu wird radiziert:
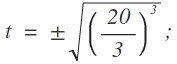
Negative Zeiten sind als Lösung nicht sinnvoll:
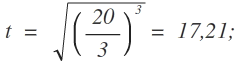
A.: Zum Zeitpunkt t = 17,2 min steigt das Wasser mit einer Geschwindigkeit von 1 cm/min.
e) Wie groß ist die mittlere Steiggeschwindigkeit des Wasserstands bezogen auf den gesamten Füllvorgang?
Da gibt es vermutlich mehrere Möglichkeiten. Ich denke es ist am einfachsten die Zeit auszurechnen, die man braucht um das gesamte Gefäß zu füllen und dann die Höhe des Gefäßes durch die Füllzeit zu teilen.
A.: Die Füllzeit beträgt 125 min (siehe b) ). Die Höhe des Gefäßes ist 100 cm. Damit ergibt sich die mittlere Geschwindigkeit zu vm= 100 /125 cm/min = 0,8 cm/min.
Noch ein Hinweis. In der Rechnung habe ich keine Einheiten verwendet, da Du sie auch in Deiner Angabe nicht verwendet hast. Erst in der Antwort habe ich sie dann wieder eingefügt.
lg JR