f(t) = t^3 - 21·t^2 + 120·t + 200
f'(t) = 3·t^2 - 42·t + 120
f''(t) = 6·t - 42
b) berechnen sie den zeitpunkt innerhalb der 12 Monate, an dem sich der Umsatz am stärksten ändert.
f''(x) = 0
6·t - 42 = 0
t = 7
c) Der Geschäftsführer ist vorsichtiger. er nimmt an, dass deer Umsatz während der betrachteten 12 Monate linear so ansteigt, dass am Anfang und am Ende des beobachtungszeitrums die Verkaufszahlen beider Prognosen gleich sind. Welche Funktion g beschreibt den Umsatz nach dieser Prognose?
f(0) = 200
f(12) = 344
g(t) = (344 - 200) / (12 - 0) * (t - 0) + 200 = 12·t + 200
d) Für welchen zeitpunkt sagen die beiden Prognosen denselben Umsatz Voraus?
f(t) = g(t)
t^3 - 21·t^2 + 120·t + 200 = 12·t + 200
t^3 - 21·t^2 + 108·t = 0
t(t^2 - 21·t + 108) = 0
t = 0 ∨ t = 9 ∨ t = 12
Zu welchem Zeitpunkt ist der Unterschied der prognostizierten Umsatzzahlen am Größten?
d(t) = f(t) - g(t) = t^3 - 21·t^2 + 108·t
d'(t) = 3·t^2 - 42·t + 108
d'(t) = 0
3·t^2 - 42·t + 108 = 0
t = 7 - √13 ∨ t = √13 + 7
t = 3.394448724 ∨ t = 10.60555127
d(7 - √13) = 163.7443331
d(√13 + 7) = -23.74433316
Der Unterschied ist nach 3.39 Monaten am größten.
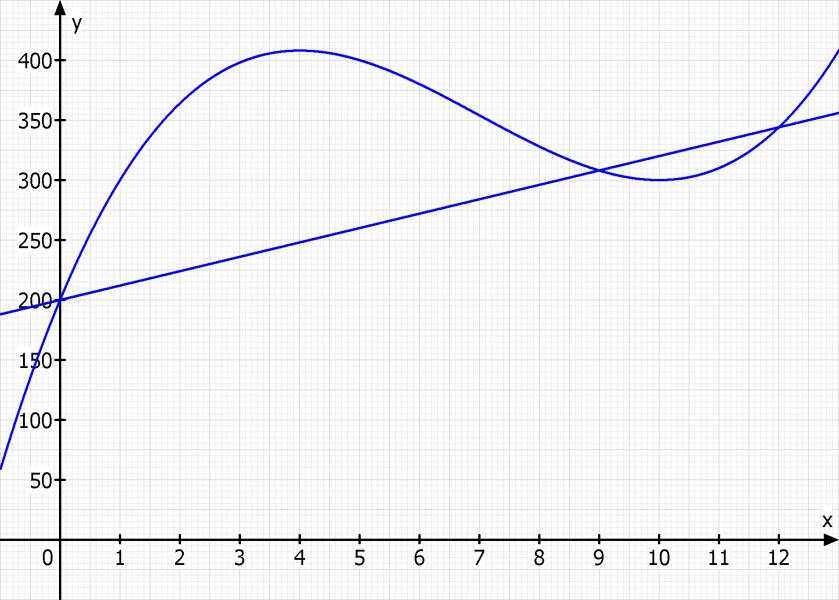
Skizze