Hallo
a) f(a) = sin ( a+c )
Welchen Einfluss hat der Summand c auf die Sinusfunktion?
Der Summand c verschiebt den Graf der Funktion sin ( a+c ) gegenüber dem Graf der Funktion sin(a) nach links, wenn c > 0 ist, und nach rechts, wenn c < 0 ist.
Untersucht die Funktionen f(a)=sin (a + 30°) und f(a)=sin ( a - 30°).
f(a)=sin (a + 30°)
Die Funktion wird um 30° nach links verschoben; das sieht dann aus wie in dem Bild unten, wobei der blaue Graph sin(x) ist und der rote Graf sin(x+pi/6). (30°/180° *pi = pi/6). Das kannst Du Dir so vorstellen: Wenn Du für x (oder a oder alpha) bei sin(x+30°) 0 einsetzt, dann erhältst Du schon den Wert, den Du bei der Funktion sin(x) erst bei x=30° erhalten hättest. In der Zeichnung kommt das einer Verschiebung des Funktionsverlaufs gleich.
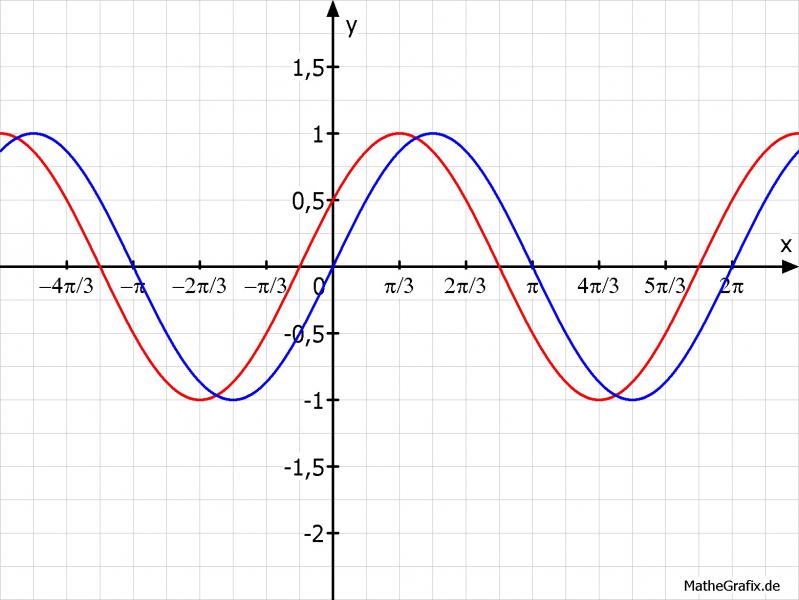
f(a)=sin ( α - 30°)
Hier wird der Graf nach um 30° oder pi/6 nach rechts verschoben: sin(x), sin(x-pi/6)
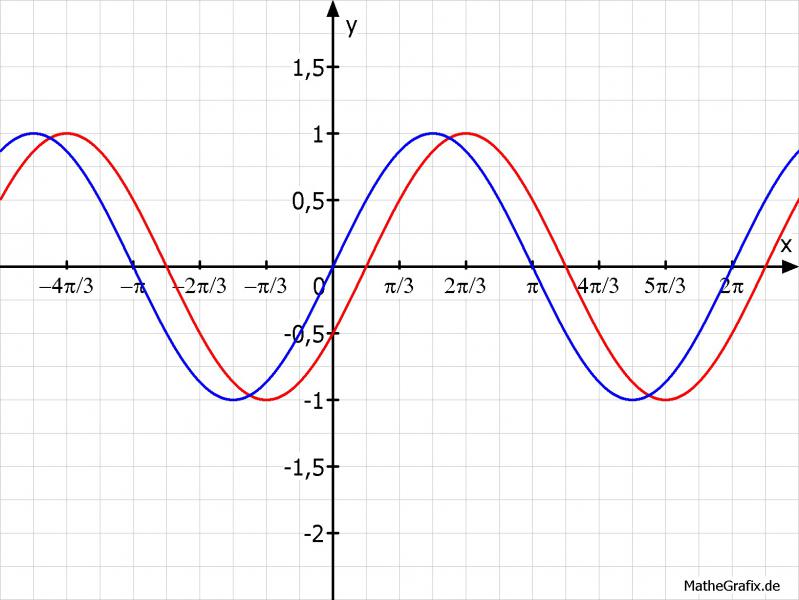
b) Die Funktionen f(a) = 2 sin (0,5(a+50*)) -1 und g(a) = -0,25 sin (2(a-60*)) +0,75 sind allgemeine Sinusfunktionen. Erklärt, wie f(a) und g(a) aus der Sinuskurve entstehen und skizziert ihren Verlauf im Koordinatensystem.
f(a) = 2*sin(0,5*(a+50°)) -1
Hier ist es schon etwas komlizierter. Ich erkläre die einzelnen Komponenten der Reihe nach. Die angesprochene Komponente ist fett gedruckt in der Gleichung.
f(a) = 2*sin(0,5*(a+50°)) -1
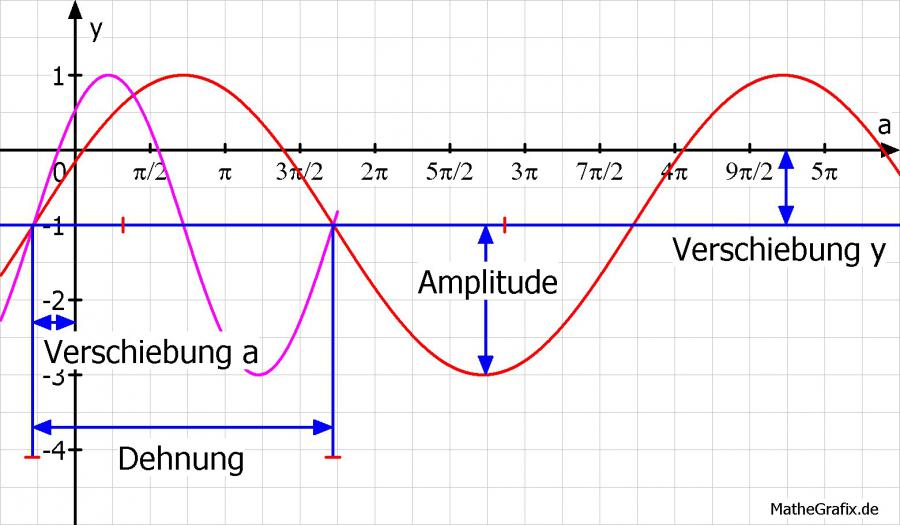
Die Amplitude der Schwingung wird hier beeinflusst und gegenüber der Funktion sin(a) um den Faktor 2 gestreckt. (siehe Amplitude)
f(a) = 2*sin(0,5*(a+50°)) -1
Die Sinuskurve wird in a-Richtung um den Faktor 2 gedehnt. f(a) = 2*sin(a+50°) -1 ist die gleiche Funktion nur ohne den Faktor 0,5. Wie Du erkennen kannst beträgt die Periode, also die Zeit oder der Wertebereich, den die Funktion für eine volltständige Schwingung braucht, jetzt das doppelte. Die Funktion ohne 0,5 vollführt eine vollständige Schwingung während die Funktion f(a) = 2*sin(0,5*(a+50°)) -1 nur eine halbe Schwingung macht. (siehe Dehnung)
f(a) = 2*sin(0,5*(a+50°)) -1
Das ist wieder eine Verschiebung. Diesmal um 50° oder 5/18*pi ≈ 0,87 gegen a-Richtung (vgl. Pfeil der a-Achse) also nach links. (siehe Verschiebung a)
f(a) = 2*sin(0,5*(a+50°)) -1
Das ist ebenfalls eine Verschiebung, allerdings gegen y-Richtung und zwar um 1. (siehe Verschiebung y)
Die zweite Aufgabe ist im Prinzip gleich. Die überlasse ich mal Dir oder vielleicht löst sie auch jemand hier aus dem Forum für Dich.
Falls Du noch Fragen hast --> Kommentar
lg JR