Ergeben die Punkte einen rechten Winkel am Punkt P2?

Question

Hallo :)

Wie kann man rechnerisch feststellen ob die drei Punkte einen rechten Winkel am Punkt P2 ergeben?

P1(2|1)  P2(3|7)  P3(8|6)

Comments

Da gab es doch mal Produkte von Vektoren ...

... wie hießen die nochmal und was hatten die für Eigenschaften ?

Answer 1

du musst überprüfen, ob    \(\overrightarrow{P_2P_1}\) •  \(\overrightarrow{P_2P_3}\) = 0 gilt.

Gruß Wolfgang

Comments

Also jeweils den Abstand zwischen P2 P1 und P2 P3 ausrechnen und dann mal nehmen, oder?

---

Ein Skalarprodukt ist nicht der Laich von Zierfischen, sondern:

https://de.wikipedia.org/wiki/Skalarprodukt

---

Was ist den jetzt eigentlich die Lösung von der Aufgabe?

Answer 2

Wie kann man rechnerisch feststellen, ob die drei Punkte einen rechten Winkel am Punkt \(P_2\) ergeben?
\(P_1(2|1)\) , \(P_2(3|7)\)  \(P_3(8|6)\)

Zeichnung, ob die unten gegebenen Berechnungen überhaupt funktionieren:

(siehe auch gegebene Kommentare)

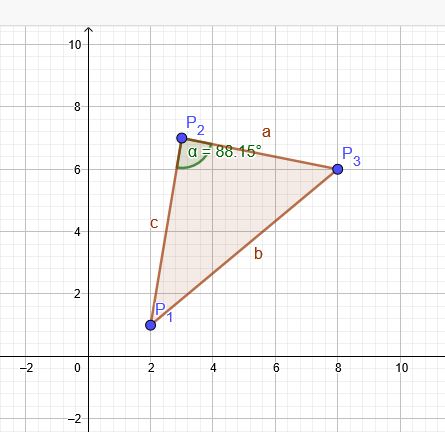
Geradensteigung durch die Punkte \(P_1(2|1)\) und \(P_2(3|7)\):

\(m_1=\frac{7-1}{3-2}=\frac{6}{1}=6\)

Geradensteigung durch die Punkte \(P_2(3|7)\) und \(P_3(8|6)\):

\(m_2=\frac{6-7}{8-3}=-\frac{1}{5}\)

1.Weg:

Falls ein rechter Winkel existiert, gilt: \( m_1\cdot m_2=-1\)

\(  6\cdot ( -\frac{1}{5}) = -\frac{6}{5}≠-1\)

oder 2. Weg:

Bestimmung des Winkels( ist oftmals noch Teil einer Aufgabe)

Allgemein: \(\tan(α)=|\frac{m_2-m_1}{1+m_2\cdot m_2}|\)

\(\tan(α)=|\frac{-\frac{1}{5}-6}{1+6\cdot(-\frac{1}{5})}  |=|-31|=31\)

\( \tan^{-1}(31)=88,15238973°≠90° \)

Comments

Funktioniert aber nicht immer, daher hier als Antwort nicht sinnvoll.

---

Funktioniert aber nicht immer, daher hier als Antwort nicht sinnvoll.

Gib mal ein Beispiel, wo es nicht funktioniert.

---

Nimm z.B. P₂(2l7)

---

Wenn es um Funktionen (tag) geht, dann sollte das immer funktionieren. Dann wäre P2(2 | 7) auch nicht erlaubt.

Ansonsten sollte man Wissen, dass eine Parallele zur y-Achse nur einen rechten Winkel bildet mit einer Parallelen zur x-Achse. Und bei P2(2 | 7) müsste P3(x | 7) gelten.

---

Es geht aber nicht um Funktionen, es geht um Punkte.

Der Ansatz von M. funktioniert nur, wenn die Steigungen existieren, was nicht immer der Fall ist.

Jetzt versucht er seine Rechnung zu retten, indem man erst mal eine Skizze machen muß, um zu sehen, ob die Rechnung erlaubt ist. Na prima…

M.: wolltest du dich nicht mal mit Vektoren beschäftigen? Damit wird es ein Einzeiler.

---

M.: wolltest du dich nicht mal mit Vektoren beschäftigen? Damit wird es ein Einzeiler.

Solche Aufgaben findet man unter anderem auch in der Mittelstufe, wo noch keine Vektorrechnung bekannt ist.

Es geht aber nicht um Funktionen, es geht um Punkte.

Mit der Begründung kann man auch sagen es geht nicht um Vektoren.

---

Werde nicht albern.

---

Ein noch möglicher Weg ist die Berechnung eines Kreises mit Mittelpunkt der Strecke b zwischen  \(P_1(\red {2}|1)\) und \(P_3(8|6)\). Das führt zum Thaleskreis. Danach Kontrolle, ob \\(P_2(3|7)\) auf diesem liegt. Ist das der Fall, dann wäre ein rechter Winkel bei  \(P_2(3|7)\) . Diese Möglichkeit haben wir dann auch im Fall von \(P_2(\red {2} | 7)\).

Answer 3

Mann könnte es mit dem Satz des Pythagoras und den Abständen der Punkte zueinander prüfen.

P1(2|1)  P2(3|7)  P3(8|6)

|P1P2|^2 = (3 - 2)^2 + (7 - 1)^2 = 1^2 + 6^2 = 37

|P2P3|^2 = (8 - 3)^2 + (6 - 7)^2 = 5^2 + 1^2 = 26

|P1P3|^2 = (8 - 2)^2 + (6 - 1)^2 = 6^2 + 5^2 = 61

|P1P2|^2 + |P2P3|^2 = |P1P3|^2

37 + 26 ≠ 61 → Es gibt keinen rechten Winkel bei P2.

Dies ist allerdings deutlich aufwändiger als mit der Steigung oder dem Skalarprodukt der Richtungsvektoren und sollte man nur machen, wenn andere Wege unbekannt sind.