Kurvendiskussion. Extrema, Wendepunkt, Nullstellen f(x) = -1/16 x^3 + 3x und g(x) =1/8 x^2

Question

Aufgabe:

Gegeben sind die Funktionen \( f \) und \( g \) durch \( f(x)=-\frac{1}{16} x^{3}+3 x \) und \( g(x)=\frac{1}{8} x^{2}(x \in \mathbb{R}) \)

a) Berechnen Sie für die Funktion \( f \) alle Nullstellen sowie die Extrem und Wendepunkte des Graphen von \( f \).

b) Berechnen Sie alle Stellen \( u \), für die die Graphen von \( f \) und \( g \) die gleiche Steigung haben.

c) Weisen Sie nach, dass es eine Stelle \( a \) gibt, an der \( f \) und \( g \) zueinander senkrechte Tangenten besitzen.

d) Vom Punkt ( \( (0|-8 \) ) aus sollen Tangenten an \( g \) gelegt werden. Ermitteln Sie Ihre Gleichungen.

e) Für jeden Wert von \( k \) mit \( 0<k<6 \) bilden die Punkte \( F(k | f(k)) \) und \( G(k | g(k)) \) mit dem Koordinatenursprung ein Dreieck. Berechnen Sie den Wert für \( k \) so, dass dieses Dreieck einen möglichst großen Flächeninhalt hat.

Comments

Hier mal die Ableitungen:

f(x) = -1/16 x^3 + 3x
f '(x) = -3/16 x^2 + 3
f''(x) = -3/8 x

g(x) =1/8 x^2
g'(x) = 1/4 x
g''(x) = 1/4

Damit kannst Du jetzt zunächst Nullstellen, Extrempunkte und Wendepunkte bestimmen.

Answer 1

Zunächst nur eine Skizze. Dann folgt die Rechnung.

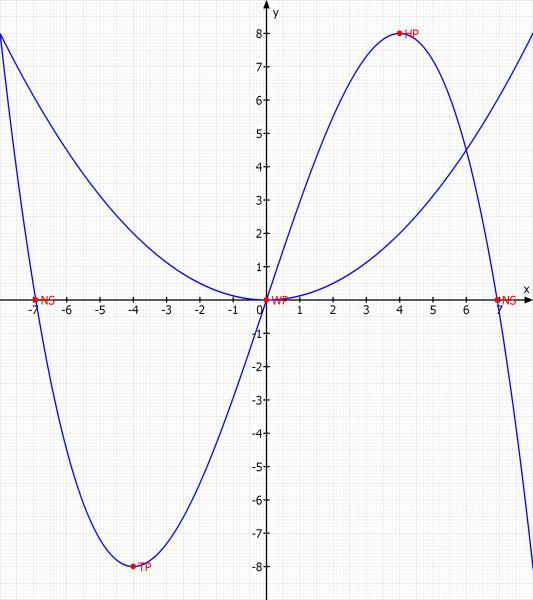
f(x) = - 1/16·x^3 + 3·x
f'(x) = 3 - 3·x^2/16
f''(x) = - 3·x/8

Nullstellen f(x) = 0

- 1/16·x^3 + 3·x = 0
x = - 4·√3 ∨ x = 4·√3 ∨ x = 0

Extremstellen f'(x) = 0

3 - 3·x^2/16 = 0
x = -4 ∨ x = 4
f(4) = 8 (Hochpunkt)
f(-4) = -8 (Tiefpunkt)

Wendestellen f''(x) = 0

- 3·x/8 = 0
x = 0
f(0) = 0 (Wendepunkt)

Aufgabe b)

f'(u) = g'(u)
3 - 3·u^2/16 = u/4
u = - 2·√37/3 - 2/3 ∨ u = 2·√37/3 - 2/3
u = -4.721841686 ∨ u = 3.388508353

Aufgabe c)

f'(a) = -1/g'(a)
3 - 3·a^2/16 = - 4/a
a = -1.579723374 ∨ a = -2.968908795 ∨ a = 4.548632170

Also hier habe ich drei Stellen und nicht nur eine.

Aufgabe d)

(g(u) - (-8)) / (u - 0) = g'(u)
(u^2 + 64)/(8·u) = u/4
u = -8 ∨ u = 8

t1(x) = g'(u) * (x - u) + g(u) = g'(-8) * (x - (-8)) + g(-8) = - 2·x - 8
t2(x) = g'(8) * (x - (8)) + g(8) = 2·x - 8

A = 1/2 * c * hc = 1/2 * (f(k) - g(k)) * k = - k^4/32 - k^3/16 + 3·k^2/2

A' = - k^3/8 - 3·k^2/16 + 3·k = 0

k = 4.206056900 ∨ k = -5.706056900 ∨ k = 0

Damit ist k etwa 4.206.