Ich zeichne mal ein kleines Bild dazu, dann wird das klarer:
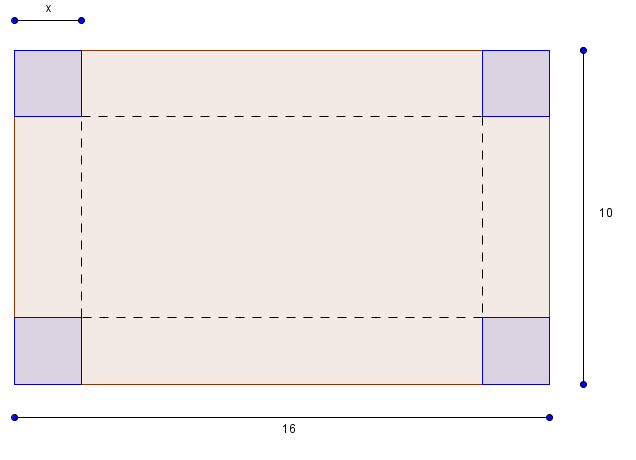
Die blauen Flächen werden herausgeschnitten und der Karton an den gestrichelten Linien geknickt.
Die Grundfläche hat also die Maße (16-2x)*(10-2x)
Die Höhe enspricht der Breite der "Seitenlappen", die hochgeklappt werden, ist also x.
Damit lautet die Formel für das Volumen:
V(x) = x*(16-2x)*(10-2x)
V(x) = (16x-2x2)*(10-2x)
V(x) = 10*(16x-2x2) - 2x*(16x-2x2)
V(x) = 160x - 20x2 - 32x2+4x3
V(x) = 4x3-52x2+160x
Um das Extremum zu bestimmen, muss V'(x) = 0 gesetzt werden:
V'(x) = 12x2-104x+160
0 = 12x2-104x + 160 | :12
0 = x2 - 26/3 x + 40/3
Lösbar z.B. mit der pq-Formel:
x1/2 = 13/3 ± √(169/9 - 120/9)
x1/2 = 13/3 ± √(49/9)
x1/2 = 13/3 ± 7/9
x1 = 20/3
x2 = 6/3 = 2
Um festzustellen, an welcher Stelle das Maximum liegt, kann die zweite Ableitung bestimmt werden. Für die Maximalstelle xmax muss V''(xmax)<0 gelten.
V''(x) =24x -104 = 4*(6x-26)
V''(x1) = 4*(6*20/3-26) = 4*(60-26) = 4*34 > 0 !
V''(x2) = 4*(6*2-26) = 4*(12-26) = -4*14 < 0 !
Also ist x2=2 die Maximalstelle.
Der Maximalwert lautet
V(2) = 2*(16-2*2)*(10-2*2)
V(2) = 2*(16-4)*(10-4)
V(2) = 2*12*6 = 12*12 = 144