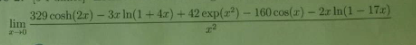
Ich hab mich anscheinend vertippt, im Zähler sollte es ln(1
+4x) sein, aber es würd mich wundern
wenn das allzu ausshlageben ist.
Hab mir einen der vorgeschlagenen Tags genommen, brauchte min. 2.
Bin dennoch für jede Belehrung dankbar, deshlab bin ich ja hier.