Was sind Randpunkte eines Definitionsbereiches? ( f (x)=(1−x )/(Wurzel (1−x^2)))

Question

Es sei f(x) := (1−x )/(Wurzel (1−x²)) gegeben.  An welchen Stellen x ∈ R ist die Funktion definiert? Berechnen Sie die Funktionengrenzwerte lim_x→x∗ fur alle Randpunkte x∗ des Definitionsbereichs.

Hier weiß ich ja, dass die Funktion für R \{1,-1} definiert ist. Jetzt würde ich gerne wissen, was mit Randpunkten gemeint ist. Meint man damit nur +/- unendlich oder eben auch +/- 1? Und müsste ich dann von jeweils allen den links- und rechtsseitigen Grenzwert bilden?

Grüße

Comments

@Wolfgang: Aber warum muss ich dann nicht den Limes von +1 berechnen?

---

du meinst lim_x→1+ f(x)

weil die Funktion für werte oberhalb von 1 nicht definiert ist. diese x-Werte sind nämlich mit 1⁺  gemeint.

---

Beziehungsweise Limes von x->+1

---

Achso, aber lim_x->1- f(x) gibt es auch nicht.  Es gibt ja nur lim für x gegen -1 von rechts und von links. Oder habe ich da jetzt was falsch verstanden?

---

"Du musst also  lim_{x→ -1+} f(x) = 0   und  im_{x→ -1-}  f(x) =  ∞  bestimmen."

Ich habe es so verstanden, dass das linke Vorzeichen beschreibt welche Zahl man genommen hat und das rechte von welcher Seite aus man nach dem Grenzwert strebt. Und deswegen fand ich es komisch, dass zweimal die -1 genommen wurde und kein einziges mal die +1, was ja auch ein Randpunkt ist.

---

Und ich würde auch gerne wissen, wie du auf die Grenzwerte gekommen bist. Beziehungsweise wie man durch Umformung der Funktion auf diese kommen kann. Ich darf L'Hospital leider nicht benutzen.

Answer 1

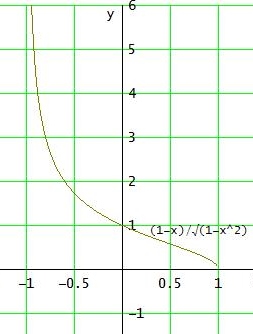
 >   f(x) := (1−x )/(Wurzel (1−x²))

der Nenner (Wurzel (1−x²)) muss ≠ 0 sein und der Radikand  unter der Wurzel ≥ 0

also muss gelten:   1−x² > 0  ⇔  x² < 1  ⇔  |x| < 1   ⇔   -1 < x < 1  ⇒  D = ] -1 ; 1 [

Die Randpunkte von D sind also x = -1 und x = 1

Du musst also  lim_{x→ -1+} f(x) = 0   und  im_{x→ -1-}  f(x) =  ∞  bestimmen.

Gruß Wolfgang