Rechtecke unter Funktionsgraphen?

Question

Nabend,

kann mir jemand bei dieser Aufgabe helfen? Ich verstehe sie nicht. Ich verstehe im Allgemeinen nicht, was einem solche Aufgaben bringen. Kann hier jemand  ebenso einen Bezug zur Wirklichkeit herstellen?

Answer 1

a)

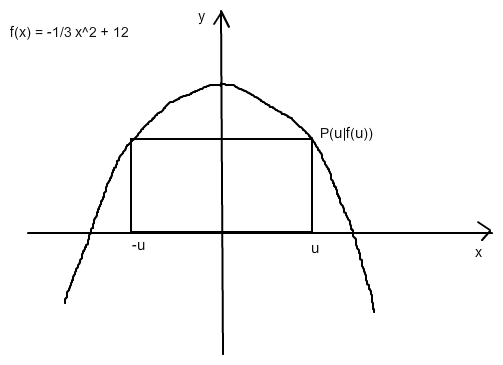
ein solches Rechteck hat den Flächeninhalt  A(u) = 2u • f(u)

→  A(u) = 2u • (-1/3·u² + 12) = -2/3·u³ + 24u

Der Flächeninhalt ist eine Funktion von u und hängt von der Wahl der x-Koordinate u ab. Wie jede Funktion hat er ein Maximum, wenn  A'(u) eine Nulltelle hat, an der A"(u) < 0 gilt:

A'(u) = -2·u² + 24 = 0 →  u = ± 2·√3

A"(u) = - 4u  →  A"( 2·√3) < 0  → für u =  2·√3 ist der Flächeninhalt maximal.

A(2·√3)  = 32·√3 ≈ 55,4 Flächeneinheiten ist der maximale Flächeninhalt.

b)

Wenn die Parabel um v nach oben verschoben wird, gilt A(u) = 2u • (-1/3·u² + 12 + v)

→  A'(u) = - 2·(u² - v - 12) = 0 →   u_max = √(v + 12) > √12 = 2·√3  

→ Das flächenmaximale Rechteck wird breiter.

Gruß Wolfgang

Answer 2

kann mir jemand bei dieser Aufgabe helfen? Ich verstehe sie nicht.
Ich verstehe im Allgemeinen nicht, was einem solche Aufgaben bringen.
Kann hier jemand  ebenso einen Bezug zur Wirklichkeit herstellen?

Dies sind sogenannte Extremwertaufgaben. Es werden die Hoch- und Tiefpunkte
einer Funktion bestimmt.

Diese Berechnungen werden in der Technik und im kaufmännischen durchgeführt
um optimale Lösung  für technische Anwendungen und den optimalen Gewinn
zu finden.

Extremwertaufgaben kommen sehr häufig vor.

Falls dir irgendetwas an der Aufgabe unklar ist dann bitte nachfragen.

Falles du weitere Aufgaben / Fragen hast dann wieder einstellen.