Schnittwinkel zwischen Ebene und Gerade

Question

Also ich habe folgende Aufgaben als Hausaufgabe aufbekommen.

a) Bestimmen Sie c so, dass der Winkel zwischen der x1,x2-Ebene und der Geraden g:x= r* (3/4/c) die Größe 45 Grad hat.

Aufgabe b): Betrachten Sie alle Ursprungsgeraden, die mit der x1,x₂=Ebene einen Winkel von 45 Grad bilden. Beschreiben Sie die Lage der Schnittpunkte dieser Geraden mit der Ebenr E: x₃₌5.

Also zu Aufgabe a habe ich nach der Formel zu Schnittwinkel sin a=c/5 aber mehr weiss ich leider auch nicht.

Danke für die Hilfe

Answer 1

a)

für den Schnittwinkel α zwischen einer Ebene und einer Geraden gilt:

sin(α) = | (Richtungsvektor u der Geraden) • (Normalenvektor n der Ebene) |  /  [ |$\vec{u}$| • |$\vec{n}$| ]

Hier:

mit   sin(45°)  =  1/2 · √2    und    |$\vec{a}$|= √( a₁² + a₂² + a₃²)   →

1/2 · √2 = | $\begin{pmatrix} 3 \\ 4 \\ c \end{pmatrix}$ • $\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ | / [ |$\vec{u}$ | · |$\vec{n}$| ]

1/2 · √2 = | c | / [ √(25 + c²) · 1 ]      | • √(25 + c²)  | • 2

√2 · √(25 + c²)  = 2·|c|   | Quadrieren

2 · (25 + c²)  = 2·|c|

 50 + 2c²  = 4c²    | - 2c²

 50 = 2c²    | : 2  |  ↔

c² = 25

c = ± 5

Nachtrag: 

b)

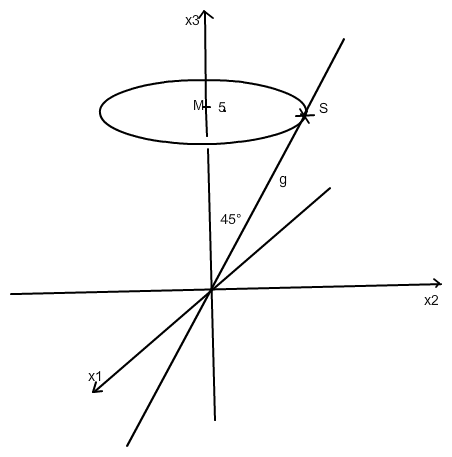
Auf dem abgebildeten Kreis liegen die gesuchten Punkte. Da das Dreieck MOS gleichschenklig ist, hat der Kreis den Radius 5. (Zeichnung nicht ganz maßstäblich :-))

Gruß Wolfgang

Answer 2

Die x-y-Ebene hat den Normalenvektor [0,0,1]

Also ist der Winkel

SIN(45°) = [3, 4, c]·[0, 0, 1]/ABS([3, 4, c])

√2/2 = c/√(c² + 25)

√(2·c² + 50) = 2·c

2·c² + 50 = 4·c²

50 = 2·c²

25 = c²

c = ± 5

Eigentlich würde nur 5 die Ausgangsgleichung erfüllen. Allerdings kann der winkel auch -45 Grad sein und daher ist auch -5 eine Lösung.

Comments

b): Betrachten Sie alle Ursprungsgeraden, die mit der x1,x₂=Ebene einen Winkel von 45 Grad bilden. Beschreiben Sie die Lage der Schnittpunkte dieser Geraden mit der Ebenr E: x₃₌5. 

Die Schnittpunkte bilden einen Kreis mit dem Mittelpunkt [0,0,5] und dem Radius 5.

---

> Eigentlich ...

Deswegen schreibt man die Formel für den Schnittwinkel im Zähler wohl besser mit  Betrag.