Ein Industriebetrieb fertigt gemäß dem abgebildeten Verflechtungsgraphen aus den Ausgangsprodukten \( A_{1}, A_{2} \) und \( A_{3} \) zunächst die Zwischenprodukte \( Z_{1}, Z_{2} \) sowie \( Z_{3} \) und daraus anschließend die beiden Endprodukte \( E_{1} \) sowie \( E_{2} \).
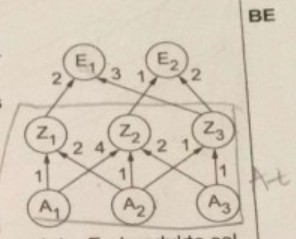
Stückzahlen der Ausgangsprodukte, der Zwischenprodukte und der Endprodukte sollen jeweils durch einen Spaltenvektor dargestellt werden. Die Verflechtungsmatrix AZ gibt zu jedem Zwischenprodukt die Stückzahlen der für ein Stück erforderlichen Ausgangsprodukte an, die Verflechtungsmatrix ZE entsprechend zu jedem Endprodukt die Stückzahlen der erforderlichen Zwischenprodukte.
a) Geben Sie \( A Z \) und \( Z E \) an.
b) Dem Industriebetrieb liegt eine Bestellung von \( 500 \mathrm{E}_{1} \) und \( 400 \mathrm{E}_{2} \) vor. Berechnen Sie die Stückzahlen der dafür erforderlichen Ausgangsprodukte.
c) Den folgenden Tabellen können für die Ausgangsprodukte und die Zwischenprodukte die dem Betrieb entstehenden Anschaffungskosten bzw. Fertigungskosten pro Stück entnommen werden:
| A1 | A2 | A3 |
| Anschaffungskosten | 2 € | 1 € | 3 € |
| Z1 | Z2 | Z3 |
| Fertigungskosten | 3,5 € | 5 € | 2 € |
Die Kosten für die Fertigung eines Endprodukts \( \mathrm{E}_{1} \) aus den Zwischenprodukten betragen sieben Euro. Ermitteln Sie die Kosten, die dem Betrieb für die Herstellung eines Endprodukts \( \mathrm{E}_{1} \) für Anschaffung und Fertigung insgesamt entstehen.
d) Der Betrieb hat \( 46 Z_{1}, 64 Z_{2} \) und \( 81 Z_{3} \) auf Lager. Bestimmen Sie, wie viele Endprodukte \( \mathrm{E}_{1} \) sich daraus höchstens fertigen lassen.
e) Beschreiben Sie für jede der Matrizen AZ und ZE, wie die Anzahl der Zeilen und die Anzahl der Spalten verändert werden müssen, wenn aus den Ausgangsprodukten ein weiteres Zwischenprodukt \( Z_{4} \) gefertigt wird, das für die Herstellung der Endprodukte verwendet wird.