Kurve: 2x2 + 2xy + 4y2 - 56 = 0. In welchem Punkt ist die Steigung 1? Tangentengleichung?

Question

Wie geht man an solch eine Aufgabe heran?

Kurve: 2x² + 2xy + 4y² - 56 = 0. In welchem Punkt ist die Steigung 1? Tangentengleichung?

Wie rechnet man solch eine Aufgabe? Muss man x=1 setzen und y ausrechnen?

 

Berechnen Sie den Punkt der durch die Gleichung

2x²+2xy+4y²-56=0

definierten Kurve, an dem die Tangente an die Kurve die Steigung 1 besitzt. Es gibt 2 solcher Punkte. Betrachten Sie nur den Punkt mit positiver x-Komponente. Geben Sie die Gleichung der Tangente an die Kurve in diesem Punkt vollständig an.

Comments

Du solltest Windows warten und ist das ein Steam-Icon rechts unten? Counter Strike? Wer nutzt denn heute noch ICQ, oh gott!

Deshalb gibt es Schreibregeln... einfach Text aus der PDF herauskopieren und einfügen! :) Wenn Adobe Reader Mist ist, nimm Foxit PDF Reader...

---

Berechnen Sie den Punkt der durch die Gleichung

2x²+2xy+4y²-56=0

definierten Kurve, an dem die Tangente an die Kurve die Steigung 1 besitzt. Es gibt 2 solcher Punkte. Betrachten Sie nur den Punkt mit positiver x-Komponente. Geben Sie die Gleichung der Tangente an die Kurve in diesem Punkt vollständig an.

---

Wie rechnet man solch eine Aufgabe? Muss man x=1 setzen und y ausrechnen?

Wenn schon müsstest du die erste Ableitung = 1 setzen. Falls du die Gleichung nach y auflösen kannst (ist eine quadratische Gleichung), kannst du sie vermutlich auch ableiten. Scheint mir aber nicht der schnellste Weg zu sein.

Habe den Text von Anonym jetzt eingefügt.

---

Es handelt sich hier um die Gleichung einer Ellipse.

Vielleicht kannst du mit den folgenden Angaben und Umformungen dieser Gleichung etwas anfangen:

https://www.wolframalpha.com/input/?i=2x%5E2+%2B+2xy+%2B+4y%5E2+-+56…

---

Der Lösungsweg ist klar, aber es gibt viel zu rechnen

1.) nach y umstellen

y = f(x) = - x / 4  - ( √ 7)  / 4 * √ ( 32 - x^2 )

2.) 1.Ableitung bilden

f ´(x) = ( √ 7 * x  ) / ( 4 * √ ( 32 - x^2 ) ) - 1/4

3.)  Steigung gleich 1

f ´(x) = 1 = ( √ 7 * x  ) / ( 4 * √ ( 32 - x^2 ) ) - 1/4

4.) x ausrechnen

x = 5

Ich habe hierzu ein CAS-Programm zum ausrechnen verwendet.

  mfg Georg

---

Welches CAS Programm verwendest du denn?

---

mathecoach @ mathecoach.de

MuPad Pro 4 von 2007

mfg Georg

Answer 1

2x² + 2xy + 4y² - 56 = 0

Zunächst mal ins das eine quadratische Gleichung die wir nach y auflösen wollen. Dazu können wir durch 4 teilen und die pq-Formel anwenden.

y² + 0.5xy + 0.5x² - 14 = 0

p = 0.5x
q = 0.5x² - 14

y = -p/2 ± √((p/2)² - q)
y = -(0.5x)/2 ± √((0.5x/2)² - (0.5x² - 14))
y = -x/4 ± √(14 - 0.4375x²)

y = - x/4 + √(14 - 0.4375·x²)
y' = - √7·x/(4·√(32 - x²)) - 1/4 = 1
x = -5

y(-5) = 3

t(x) = 1(x + 5) + 3

y = - x/4 - √(14 - 0.4375·x²)
y' = √7·x/(4·√(32 - x²)) - 1/4 = 1
x = 5

y(5) = -3

t(x) = 1(x - 5) - 3

Skizze:

Answer 2

Annahme du kommst irgendwie auf die impliziten Ableitungen. Z.B. ∂y(x)/∂x , so kann man diese = 1 setzen.

Deshalb

2x+y = -x - 4y

3x = - 5y.

x= (-5/3) y

in die Kurvengleichung einsetzen

2(5/3 y)² - 10/3 y² + 4y² = 56

(50/9 - 10/3 + 4)y² = 56

---> y = ±3

Einsetzen -----> 

x=±5

Somit x=5 und y=-3 gesuchter Punkt. (vgl. anderen Rechenweg von Georgborn)

Tangentengleichung.

y = 1*x + q       , (5|-3) einsetzen

-3 = 5+q

-8 = q

Tangentengleichung y = x-8

Comments

Ich hab mir inzwischen angeschaut, wie Wolframalpha diese impliziten Ableitungen bestimmt.

Das ist eigentlich ganz einfach:

Beachte, dass in der Schritt für Schritt-Lösung jeder Schritt erklärt wird, aber in der nächsten Zeile oft noch umgeordnet wird. Die Ausschnitte sind z.T. überlappend. Sollten aber vollständig sein.

https://www.wolframalpha.com/input/?i=implicite+derivation+2x%5E2+%2…

Hier die Version, in der y als Funktion von x als y(x) betrachtet wird. x ist einfach x.

Die Ableitung von x² ist 2x, der Summand rutscht bei WolframAlpha nach hinten. Deshalb gleich nochmals reinkopiert:

---

Zum Bestimmen von y'(x) benutzt man ganz einfach den Satz von der impliziten Funktion.

---

@ Ché Netzer: Danke für die Info. Kommt denn bei den impliziten Ableitungen zwingend der Kehrwert raus? 

F(x,y) = 2x² + 2xy + 4y² - 56 = 0

∂F/∂x = 4x + 2y

∂F/∂y = 2x + 8y

y'(x) = - 1/(2x+8y) * (4x +2y) = - (4x+2y)/(2x+8y) = -(2x+y)/(x+4y)

Gemäss Formel in Zusammenfassung hier: https://de.wikipedia.org/wiki/Satz_von_der_impliziten_Funktion#Satz_…

---

Wie meinst du das? Ob y'(x) der Kehrwert von x'(y) ist, wenn man nach beiden Variablen auflösen kann? (das ist dann einfach die Ableitung der Umkehrfunktion) Oder ob y'(x) immer [wenn F_y ungleich null] -F_x/F_y ist? Ja, das ist die Aussage des Satzes.

Oder welchen Kehrwert meinst du?

Answer 3

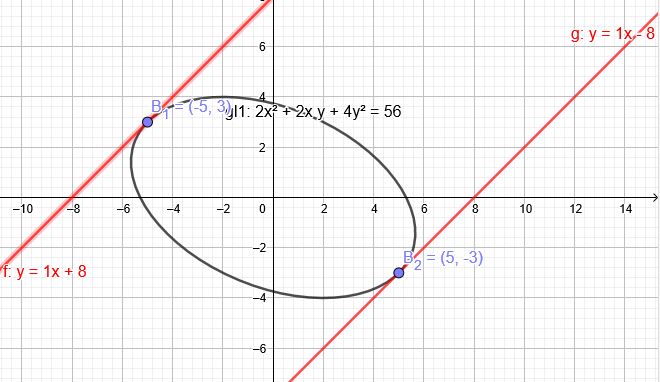
$f(x,y)=2x^2 + 2xy + 4y^2 - 56$

implizites Differenzieren:

Allgemeine Formel:

$f_x(x,y)=4x + 2y$

$f_y(x,y)= 2x + 8y$

$\frac{dy}{dx}=-\frac{f_x(x,y)}{df_y(x,y)}$

$\frac{dy}{dx}=-\frac{4x + 2y}{2x + 8y}=-\frac{2x + y}{x + 4y}$

Steigung der Tangente ist $m=1$

$-\frac{2x + y}{x + 4y}=1$

$x+4y= -2x-y$

$3x+5y=0$

$y=- \frac{3}{5}x$ Diese Gerade nun mit der Ellipse $2x^2 + 2xy + 4y^2 = 56$ schneiden:

$2x^2 + 2x(- \frac{3}{5}x )+ 4\cdot (- \frac{3}{5}x) ^2 = 56$

$x_1=-5$    einsetzen in  $2x^2 + 2xy + 4y^2=56$   $50 -10y + 4y^2=56$   

$y_1=-0,5$ bzw $y_1=3$ 

$x_2=5$ einsetzen in $2x^2 + 2xy + 4y^2=56$   $50 +10y + 4y^2=56$ 

$y_2=0,5$  bzw $y_2=-3$

Kontrolle welche Punkte gelten:

1.)$\frac{dy}{dx}=-\frac{2\cdot (-5) -0,5}{-0,5 -2}$   Steigung ist nicht 1

Somit ist $B_1(-5|3)$  und $B_2(5|-3)$

Jetzt die Tangenten über die Punkt-Steigungsform berechnen.

Comments

implizites Differenzieren:

das ist ja schon mal gut ...

Allgemeine Formel:$f_x(x,y)=4x + 2y \quad f_y(x,y)= 2x + 8y$

aber warum so umständlich? Leite nach $x$ ab und $y$ ist dann von $x$ abhängig - also:$$\begin{aligned} 2x^{2} + 2xy + 4y^{2} - 56 &= 0 &&\left|\, \frac{\text{d}}{\text{d} x}\right.\\ 4x+2y+2xy' +8yy' &= 0 &&\left|\, y'=1 \right.\\ 6x+10y &= 0 \\ y &= -\frac{3}{5}x\\ \implies 2x^{2} - \frac{6}{5}x^2 + \frac{36}{25}x^{2} - 56 &= 0 \\ \frac{56}{25}x^2 - 56 &= 0 \\ x_{1,2} &= \pm5 &&\implies y_{1,2} = \mp 3\\ \end{aligned}$$

---

Danke dir für die Erläuterung!