Funktion, Amplitude, Periode

Question

Gegeben ist di Funktion f (x) = 2 sin (πx) - 2 und x ∈ (-2;4)

1. Zeichne die Funktion f.

2. Gib die Amplitude und die Periode der Funktion f an.

3. Berechne im angegebenen Intervall die Schnittpunkte des Schaubildes der Funktion f mit den Koordinatenachsen

Comments

hier wurde es dir bereits ausgiebig erläutert:

https://www.mathelounge.de/395092/gegeben-ist-die-funktion-mit-2sin-pi-und-zeichne-die-funktion

Willst du von den Antworten profitieren im Sinne von Lernen oder im Sinne von jemand macht die Hausaufgaben?

Answer 1

1)

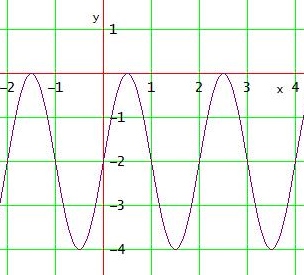
Sinnvoller wäre natürlich eine Zeichnung nach der Rechnung, aber mein Rechner kann das auch so :-):

2)

f (x) = 2 •  sin ( π • x ) - 2           und x ∈ (-1;4)

f(x) = a • sin( b • x + c ) + d   

Diesmal sind alle Punkte um  -2  in y-Richtung (also nach unten) verschoben.

An der Amplitude und der Periode ändert sich nichts:

Amplitude = |a|  = 2

Periode = 2π / b  =  2π / π  =  2 

3)

Der Schnittpunkt von f mit der y-Achse ergibt sich mit x= 0 und  f(0) = -2 zu 

           S_y(0|-2)

Die Schnittpunkte mit der x-Achse sind hier die Nullstellen von f, weil die "normalen" Extrempunkte mit dem y-Wert 2 genau um 2 nach unten verschoben sind:

2 •  sin ( π • x ) - 2 = 0

 sin ( π • x )  = 1 

 π • x  =  π/2 + k • 2π   mit  k∈ℤ

x =  1/2 + 2 • k   mit  k∈ℤ   sind also die Nullstellen in ℝ  

Gesucht sind die Nullstellen  in [ -2 ; 4 ] :

k = -1   →  x₁ = - 1,5

k = 0    →  x₂ =  0,5

k = 1    →  x₃ =  2,5 

Gruß Wolfgang