Übersetzen in mathematische Bedingungen (Kurvendiskussion rückwärts)

Question

kann mir jemand helfen aus folgenden Aufgaben die bedingungen raus zu lesen?

1.) Der Graph einer ganzrationalen Funktion 3. Grades hat den Hochpunkt HP(0|5) und den Wendepunkt WP(1|3).

2.) Eine Polynomfunktion 3. Grades hat im Punkt P(0|5/3) die Steigung k=3 und im Punkt P(-1|10) einen Extremwert.

3.) Der Graph einer Funktion 3. Grades berührt die x-Achse im Punkt P (2|0) und hat bei WP (1|3) einen Wendepunkt.

Daanke :)

Answer 1

Hi

1)

f(0) = 5      (HochPUNKT)

f'(0) = 0      (Bedingung für Hochpunkt)

f(1) = 3      (WendePUNKT)

f''(1) = 0     (Bedingung für Wendepunkt)

2)

f(0) = 5/3   (P)

f'(0) = 3       (Steigung in P)

f(-1) = 10     (Q)

f'(-1) = 0       (Bedingung für Extrempunkt)

3)

f(2) = 0    (P)

f'(2) = 0   (Berühren der x-Achse bedeutet,.dass die Steigung 0 sein muss)

f(1) = 3    (WendePUNKT)

f''(1) = 0   (Bedingung für Wendepunkt)

Schau Dir das bitte genau an. Ist immer nach dem gleichen Prinzip und nicht unwichtig ;).

Grüße 

Answer 2

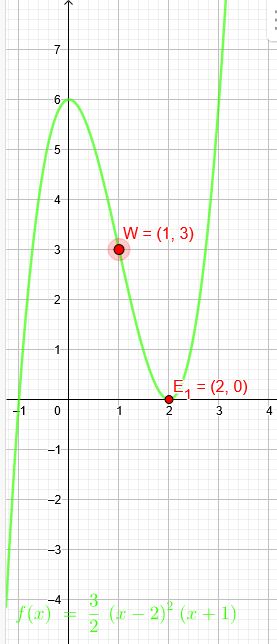
3.) Der Graph einer Funktion 3. Grades berührt die x-Achse im Punkt \(P (2|0)\) und hat bei \(W (1|3)\) einen Wendepunkt.

Weg, ohne Bedingungen aufstellen (sind schon aufgestellt worden.):

Bei \(x=2\) ist eine doppelte Nullstelle (1. Extremstelle)

Durch \(W (1|3)\)  liegt der zweite Extrempunkt bei \(E(0|6)\).

\(f(x)=a\cdot(x-2)^2\cdot(x-N)\)

\(W (1|3)\):

\(f(1)=a\cdot(1-2)^2\cdot(1-N)=a\cdot(1-N)=3\) → \(a=\frac{3}{1-N}\)

\(f(x)=\frac{3}{1-N}\cdot(x-2)^2\cdot(x-N)\)

\(E(0|6)\):

\(f(0)=\frac{3}{1-N}\cdot(0-2)^2\cdot(0-N)=\frac{12N}{N-1} =6\)

\(N=-1\)                \(a=\frac{3}{2}\)

\(f(x)=\frac{3}{2}\cdot(x-2)^2\cdot(x+1)\)