Betragsgleichung lösen mit mehreren Beträgen: |x-3| - |2x +4| = 0 und |x - 5| + |x + 1| - 2|x - 2| = 1

Question

Aufgabe:

e) |x-3| - |2x +4| = 0

f) |x - 5| + |x + 1| - 2|x - 2| = 1

Ich würde mich sehr über einen nachvollziehbaren Lösungsweg freuen.

Answer 1

bei Betragsgleichungen (EDIT: Ungleichungen durch Betragsgleichungen ersetzt) ist stets zu unterscheiden, ob der Term innerhalb der Betragsstriche positiv oder negativ ist. An den Stellen, an denen der Term =0 ist, liegt eine Unstetigkeitsstelle vor. Links und rechts der Unstetigkeitsstelle ist eine gesonderte Rechnung aufzustellen.

Beispiel: $|x-5|=1$. Für $x=5$ wird der Term innerhalb der Betragsstriche =0, also ist für links von der Stelle - d.h. $x<5$ und rechts von der Stelle - also $x \ge 5$ jeweils eine Gleichung aufzustellen. Für $x < 5$ ist der Term negativ, durch die Betragsstriche wird er wieder positiv, man schreibt:

$$-(x-5) = 1 \quad x < 5$$

das Minuszeichen macht aus dem negativen Ausdruck $x-5$ - negativ, da $x<5$ - einen positiven Ausdruck, genau wie es die Betragsstriche tun würden. Die Lösung ist $x=4$. Wichtig: Die Lösung muss(!) in dem angenommen Definitionsbereich - hier $x<5$ - liegen; ansonsten wäre es keine Lösung. Hier ist es aber erfüllt, da $x=4<5$.

Für die rechte Seite schreibt man entsprechend

$$x-5 = 1 \quad x \ge 5$$

Die Lösung wäre $x=5$ und diese Lösung liegt auch im angegebenen Definitionsbereich $x=6 \ge 5$, ist also gültig. Graphisch lässt sich das ganze so darstellen:

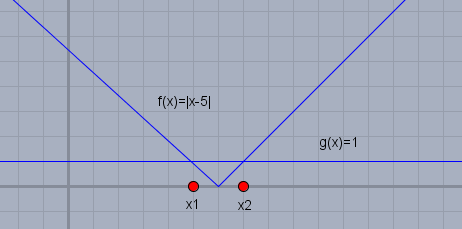
Man sieht die Funktion $f(x)=|x-5|$ mit der Unstetigkeitsstelle bei 5 (Knick) und die rechte Seite der Gleichung $g(x)=1$. Beide Funktionen schneiden sich in $x_1=4$ und $x_2=6$. Das sind die beiden Lösungen der Gleichung.

Bei der Gleichung

$$|x-5| + |x+1| -2|x-2| = 1$$

gibt es drei Unstetigkeitsstellen bei 5, -1 und 2. Diese Stellen teilen den Zahlenbereich von $-\infty$ bis $+\infty$ in die vier Bereiche $x < -1$, $-1 \le x < 2$, $2 \le x < 5$ und $x \ge 5$.

$$x < -1: \quad -(x-5) - (x+1) + 2(x-2) = 1$$

$$-1 \le x < 2: \quad -(x-5) +(x+1) +2(x-2) =1$$

$$2 \le x < 5: \quad -(x-5) +(x+1) -2(x-2) =1$$

$$x \ge 5: \quad +(x-5) +(x+1) -2(x-2) =1$$

Aus der ersten Gleichung erhält man $0 =1$ d.h. hier gibt es keine Lösung. Aus der zweiten Gleichung folgt $2x+2=1$ d.h. $x_1=-0,5$ und aus der dritten folgt $x_2=4,5$. Die letzte Gleichung ergibt wieder keine Lösung. Die Graphik macht es vielleicht klarer:

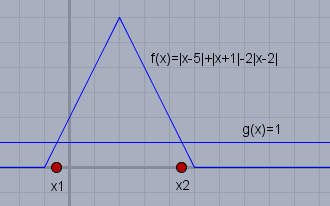
dort sieht man das die Funktion $f(x)$ jenseits von -1 und 5 immer den Wert 0 annimmt. Somit gibt es dort auch keinen Schnittpunkt mit der Geraden $g(x)=1$.

Gruß Werner

Comments

> Man sieht die Funktion f(x)=|x−5|f(x)=|x−5| mit der Unstetigkeitsstelle bei 5     (Knick) 

Das ist wohl nicht richtig

---

Dessen bin ich mir bewußt. Ich hatte ein Wort gesucht, was den 'Knick' beschreibt. Korrekt ist hier, dass an dieser Stelle die erste Ableitung nicht mehr stetig ist. Links und rechts vom Knick liegen eben zwei verschiedene lineare Funktionen vor. Folglich müssen beide Fälle unterschieden werden.

Die resultierende Funktion ist aber noch stetig - im Sinne der mathematischen Definition von 'stetig' -  wie Du richtig angemerkt hast.

Answer 2

e.)
|x-3| - |2x +4| = 0

| x - 3 | =  |2x + 4 |
Es gilt dann auch folgende Aussage
( x - 3 )²  = ( 2x +4 )²

Beispiel
| -4 | = | 4 |
( -4 )² = ( 4 ) ²

( x - 3 )²  = ( 2x +4|  )²
x² - 6x + 9 = 4x² + 16 x + 14
3x² + 22x + 5 = 0

x = -0.235
x = -7.1

Probe durchführen, Durch das Quadrieren kann es
zu Scheinlösungen kommen.

x = -0.235

Comments

Der Term x² - 6x + 9 = 4x² + 16 x + 14 ist falsch. Es muss heißen x² - 6x + 9 = 4x² + 16 x + 16

Es gibt genau eine Lösung. Sie liegt im Intervall $[-2 ; 3)$ - also

$$-(x-3)-(2x+4)=0 \quad \Rightarrow -3x+1=0 \quad \Rightarrow x=-\frac{1}{3}$$

---

Danke für den Fehlerhinweis

|x-3| - |2x +4| = 0

x = -1/3
|-1/3-3| - |2*(-1/3 +4| = 0
abs(-10/3) - abs(10/3) = 0

Es gibt noch eine 2.Lösung
2.Lösung
x = -7
| -7 -3 | - | 2 *(-7) + 4 |
| -10 | - | -10 | = 0