Multiplikation Einheitsmatrix

Question

Ich brauche Hilfe bei der Aufgabe.                                         

Multiplizieren sie \( A \) von links und von rechts
jeweils mit einer passenden Einheitsmatrix.
a) \( A=\left(\begin{array}{ccc}{6} & {1} & {2} \\ {4} & {-3} & {0}\end{array}\right) \quad \)

b) \( A=(8,2) \)

c) \( A=\left(\begin{array}{c}{6} \\ {-4} \\ {3}\end{array}\right) \)

d) \( A=\left(\begin{array}{cc}{4} & {1} \\ {0} & {-3} \\ {-4} & {6}\end{array}\right) \)

e) \( A=\left(\begin{array}{ccc}{3} & {0} & {5} \\ {-2} & {1} & {7} \\ {6} & {0} & {-8}\end{array}\right) \)

\( f) A=\left(\begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right) \) 

Answer 1

probe,

zwei Matrizen A und B können miteinander multipliziert werden, wenn die Spaltenanzahl von A der Zeilenanzahl von B entspricht. Daraus ergeben sich folgende Produkte:

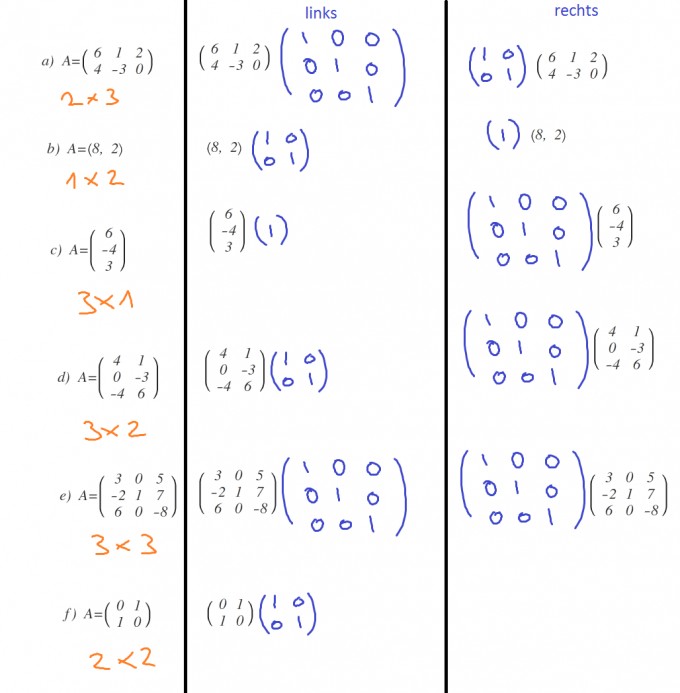
Du erhältst bei den Multiplikationen immer wieder die Matrix A als Ergebnis. Die Einheitsmatrix ist übrigens das neutrale Element bezüglich der Multiplikation über dem Ring der quadratischen Matrizen.

Konnte ich Dir damit weiterhelfen? Melde Dich gerne wieder, wenn Du Rückfragen hast.

André, savest8

Comments

da die Einheitsmatrix das neutrale Element bezüglich der Multiplikation ist.

Von welcher algebraischen Struktur sprichst du hier ?

---

Von dem Ring der quadratischen Matrizen.

---

Die As aus dem Beispiel gehören aber größtenteils gar keinem solchen Ring an.

---

Das ist richtig, weil die As größtenteils nicht quadratisch sind. Die Aussage ist im Kern korrekt ... vielleicht sollte ich die Folgerung "da" rausnehmen. Interessant ist diese Eigenschaft dennoch.

---

             

Answer 2

Das Produkt AB einer m×n-Matrix A und einer n×p-Matrix B ist eine m×p-Matrix. Matrizen, die nicht in dieser Weise zusammenpassen, kann man gar nicht multiplizieren. Bei der Aufgabe sollst Du zeigen, dass Du das mitgekriegt hast.

Comments