Anwendungen der Differenzialrechnung Beispiel mit Wasserstand

Question

Nach heftigen Unwettern wurde eine Kleinstadt durch einen Fluss überflutet. Die Höhe h (in cm) des Wasserstands in der Stadt lässt sich durch die folgende Funktion annähernd beschreiben:

h(t) = (2/27)*t^4-(16/9)*t^3+(32/3)*t^2+24           0d≤t≤12d               

t..... Zeit in Tagen (d) nach Beginn der Messung

1)Die Bevölkerung konnte mit den Aufräumungsarbeiten beginnen, als der Wasserstand weniger als 30cm betrug. Am wievielten Tag nach Beginn der Messung konnten daher die Arbeiten beginnen?

Comments

EDIT: Wasserstrand durch Wasserstand ersetzt in Text und Überschrift. 

Es handelt sich um eine Wassertiefe und keine Strandlinie. So ähnlich wie der Pegelstand eines Sees. Habe diese beiden Tags ergänzt. 

Vielleicht hilft dir das schon mal um die Frage zu begreifen. 

Answer 1

Das ist keine Aufgabe für die Differentialrechnung.

Die Grafik zeigt das ab  ca 11 Tag der Pegel
unterhalb von 30 cm liegt. ca 11.2

Willst du genauer rechnen kann z.B. das
Newton-Verfahren benutzt werden.

mfg Georg

Comments

das Newton-Verfahren benutzt werden.

Und dann wäre es doch Differentialrechnung.

Answer 2

hier ist die Rechnung:

Answer 3

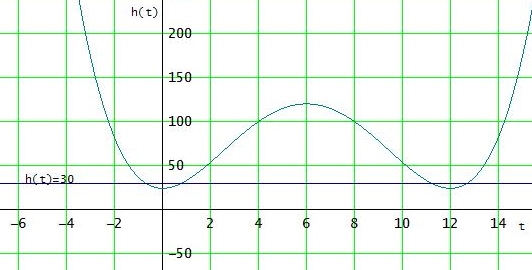
man muss die Ungleichung   

h(t) = (2/27)*t⁴-(16/9)*t³+(32/3)*t²+24 > 30 lösen   (#)

⇔  (2/27)*t⁴-(16/9)*t³+(32/3)*t² - 6 > 0

⇔  t⁴ - 24·t³ + 144·t² - 81 > 0 

Wir betrachten fx) =  x⁴ - 24·x³ + 144·x² - 81 

Wir bestimmen die Nullstellen von f(x) und erhalten aus der W-Form des Graphen den Vorzeichenverlauf von f(x) und damit die Lösungsmenge von #.

 x⁴ - 24·x³ + 144·x² - 81 = 0 

Solche Gleichungen kann man i.A. nur aufwändig nach x auflösen:

http://www.mathe.tu-freiberg.de/~hebisch/cafe/viertergrad.pdf

Deshalb benutzt man meist ein Näherungsverfahren, zum Beispiel das

Newtonverfahren:

Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man immer bessere Werte mit der Formel

x_neu =  x_alt - f(x_alt) / f ' (x_alt)

Starwert x=-1

x	f(x)	f '(x)
-1	88	-364
-0,758241758	12,58301904	-261,5123724
-0,710125415	0,464760328	-242,2565459
-0,708206952	0,000729119	-241,4965372
-0,708203933	1,80485E-09	-241,4953416
-0,708203932	0	-241,4953416

Starwert x = 1

x	f(x)	f '(x)
1	40	220
0,818181818	2,699815586	189,6288505
0,803944451	0,018122171	187,0789239
0,803847582	8,44489E-07	187,061488
0,803847577	0	187,0614872

Starwert x = 10

x	f(x)	f '(x)
10	319	-320
10,996875	40,68826111	-220,4869142
11,18141321	2,776623992	-189,7010118
11,19605006	0,019149768	-187,0799125
11,19615242	9,42968E-07	-187,0614881
11,19615242	-3,63798E-12	-187,0614872

Starwert  x = 15

x	f(x)	f '(x)
15	1944	1620
13,8	536,0256	775,008
13,1083612	130,0860006	413,1038048
12,79346214	22,04539718	275,8452117
12,71354269	1,29493352	243,611786
12,70822713	0,005602645	241,5045286
12,70820393	1,06564E-07	241,4953417
12,70820393	-7,27596E-12	241,4953416

Der Wasserstand st zum erstenmal nach ≈ 11,2 d  unter 30 cm     

Graph von h(t)


                        Gruß Wolfgang

Comments

Hallo Wolfgang,

du bist Lehrer, ja ?

Was hältst du von der Aufgabe ?

Soll damit das Newton-Verfahren geübt werden ?
Dies wäre aber zu Fuß eine Menge Arbeit !

Am wenigsten Arbeit hätte man bei
- Grafik zeichnen ( siehe meine )
- Startwert ablesen
- CAS mit Newton-Verfahren verwenden
Zeit 5 min.

Es macht keinen Sinn alles zu Fuß zu berechnen.
Soweit meine Einschätzung.

mfg Georg

---

In der Schule würde ich die Aufgabe nicht stellen.

In Klausuren sind oft nur "normale" Taschenrechner zugelassen.

---

h(t) = (2/27)*t⁴-(16/9)*t³+(32/3)*t²+24 = 30

ich bin nicht so informiert. Gibt es schon
Taschenrechner die obige Gleichung auf
Tastendruck lösen können ?