Konstruktion eines ähnlichen Trapezes

Question

Bei Aufgabe5 (tut mir leid ist ein bisschen unscharf). Aber ich schreibe nochmal die Aufgabe ab.

a) Die Strecke x soll das gegebene Trapez in zwei zu einander ähnliche Trapeze zerlegen.

b) Konstruieren Sie ein zum gegebenen Trapez ähnliches Trapez, dessen Flächeninhalt das 16/9-fache des gegebenen Trapezes beträgt. 

zu a) dachte ich mir ich konstruiere eine parallele Strecke zur  Grundlinie und erhalte dann ähnliche Trapeze aber warum?

zu b) bin ich überfragt ich habe die Seiten gemessen (c=8, b=4, a= 3.5) und kann ich dann den Flächeninhalt berechnen. Aber dann weiter weiss ich nicht. 

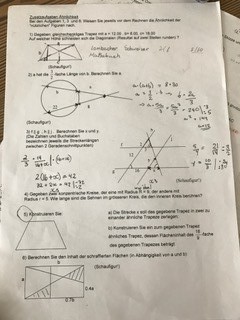
Bei Aufgabe5 (tut mir leid ist ein bisschen unscharf). Aber ich schreibe nochmal die Aufgabe ab.

a) Die Strecke x soll das gegebene Trapez in zwei zu einander ähnliche Trapeze zerlegen.

b) Konstruieren Sie ein zum gegebenen Trapez ähnliches Trapez, dessen Flächeninhalt das 16/9-fache des gegebenen Trapezes beträgt. 

zu a) dachte ich mir ich konstruiere eine parallele Strecke zur  Grundlinie und erhalte dann ähnliche Trapeze aber warum?

zu b) bin ich überfragt ich habe die Seiten gemessen (c=8, b=4, a= 3.5) und kann ich dann den Flächeninhalt berechnen. Aber dann weiter weiss ich nicht. 

Comments

a) Die Strecke x soll das gegebene Trapez in zwei zu einander ähnliche Trapeze zerlegen.

Strecke ist nicht im Bild zu erkennen. Ist es ein gleichschenkliges Trapez? Soll die Strecke horizontal verlaufen? 

b) Konstruieren Sie ein zum gegebenen Trapez ähnliches Trapez, dessen Flächeninhalt das 16/9-fache des gegebenen Trapezes beträgt. 

zu b) bin ich überfragt ich habe die Seiten gemessen (c=8, b=4, a= 3.5) und kann ich dann den Flächeninhalt berechnen. Aber dann weiter weiss ich nicht. 

Bei zentrischer Streckung entstehen "ähnliche Figuren". 

Bei einem Streckungsfaktor k wird die Fläche mit dem Faktor k^2 multipliziert. 

Um also k zu bekommen, rechnest du k = √(16/9) = 4/3 . 

Also: Zentrische Streckung mit k=3/4 durchführen. Messen musst du da nichts!

Du kannst z.B. die Ecke A als Streckzentrum wählen und dann mit einem Hilfstrahl die Strecken AB, AC und AD wie verlangt strecken. (Grundkonstruktion Streckenteilung / Streckung nachschauen, wenn nicht mehr präsent)

Answer 1

Zu a) Die Idee mit der Parallelen zur Grundlinie ist schon richtig. Aber in welchen Abstand zur Grundlinie muss dies Parallele liegen? Zur Beantwortung dieser Frage verlängere die nicht-parallelen Seiten des Trapezes so, dass sie sich in einem Punkt Z schneiden. Wähle Z als Zentrum einer zentrischen Streckung.

Zu b) Zur Konstuktion einer 16/9 mal so großen Fläche muss eine zentrische Streckung mit dem Sreckfaktor 4/3 durchgeführt werden. Wähle als Streckzentrum einen Eckpunkt des gegebenen Trapezes.

Comments

Dann ist die obere seite des gegebenen Trapezes die gesuchte Strecke x nicht wahr? Oder lieg ich komplett falsch?

---

Ich habe jetzt die zwei schenkel gemessen die neu entstanden sind zum Punkt Z

Dann kann ich doch den streckungsfaktor von den schenkeln ausrechnen und den für die anderen seiten anwenden?

---

Wenn du mir die Maße des Trapezes und der Verlängerungen bis Z mitteilst, kann ich dir helfen.

---

ja gerne mache ich das.

die Grundseite ist 5 die parallele dazu 2.8 die Schenkel jeweils 3 und die Verlängerung zum Punkt Z ist jeweils 3.7 

dann wäre doch der streckungsfaktor 3.7/3 also 1.23?

---

Wenn du mir die Maße des Trapezes  ...

Unsinn !
Du solltest beachten, dass es ums Konstruieren und nicht ums Messen geht.

---

Was muss ich dann machen? Ich muss ja den streckungsfaktor wissen.

---

Also allgemein: Damit die Trapeze ähnlich sind, muss eine Parallele zu Grundseite mit der Länge x gezeichnet werden und es muss gelten: c/x=x/a. (a ist die Länge der Grundseite und c ist die Länge der dazu parallelen Seite). Also muss x²=a·c sein. Ein solches x kann man mit Hilfe des Höhensatzes von Euklid konstruieren (a und c als Hypotenusenabschnitte).

---

Hallo Roland

Der Lehrer hat gesagt mit dem Punkt suchen etc das ist nicht genügend sondern dein Weg ist der Richtige. Meinst du kannst mir das genau zeigen? Mit dem Höhensatz und Thaleskreis das flächengrössete Trapez zu konstruieren.

Hoffentlich kannst du mir helfen.

---

Zeichne eine Hypotenuse der Länge a+c (a und c sind die beiden Hypotenusenabschnitte). Schlage den Thaleskreis mit dem Durchmesser a+c. Errichte im Punkt H , wo a und c aneinanderstoßen die Senkrechte (auf a, auf c oder auf a+c). Diese Senkrechte schneidet den Thaleskreis in C. Dann ist x=HC.

---

Hallo Roland 

 

Wie würde ich dabei den 16/9 fachen grösseren Flächeninhalt einbringen für die Konstrultion?

---

Der Streckfaktor müsste 4/3 sein. Im Falle des Trapezes klappt das im allgemeinen nicht sondern nur, wenn a/c =16/9 ist.

---

Wie kann die Strecke x jetzt senkrecht, wenn du als erstes gesagt hast die Strecke x sei parallel zu der Grundseite?

---

Wo habe ich denn gesagt, dass die Strecke x jetzt senkrecht zu der Grundseite sein muss?

---

Das HC ist x und da dachte ich, dass diese senkrecht zu der Grundseite ist.

Weil ac is die Hypotenuse 

---

Oder zeichne ich erst die parallele x ein und verlängere diese zu der Länge ac und wende dann den Thaleskreis an und dann den Höhensatz?

---

a und c sind die Längen der gegenüberliegenden parallelen Trapezseiten.

---

Das weiss ich. Und dazwischen zeichne ich die Parallele x. 

Und dann wende ich den thaleskreis an und den höhensatz oder?

---

Kannst du eventuell eine Zeichnung hochladen, weil ich würde es wirklich gerne verstehen. Komme aber nicht mit der Konstruktion klar...

---

Leider weiß ich nicht, wie man Zeichnungen hochläd. Deshalb hier nochmal eine genaue Beschreibung des Vorgehens:

Erster Schritt: Streckenlängen kann man in den Zirkel nehmen und an jede Stelle der Zeichenebene übertragen.  Zeichne eine Gerade g und trage auf ihr a = AB und c = CD so ab, dass die beiden Strecken in einem Punkt H aneinanderstoßen. Nenne die Endpunkte der Gesamtstrecke A und D. Schlage den Thaleskreis mit dem Durchmesser AD (Länge a+c). Errichte im Punkt H , wo a und c aneinanderstoßen die Senkrechte (auf AD). Diese Senkrechte schneidet den Thaleskreis in E. Dann ist x=HE. 

Zweiter Schritt: Übertrage x zunächst von A aus auf AB und nenne dort x = AF. Eine Parallele zu AD durch F schneidet BC in G. Eine Parallele durch G zu AB schneidet AD in J. Dann ist JG die gesuchte Teilstrecke, sodass zwei zueinander ähnliche Teiltrapeze entstehen.

---

Danke ich habe dazu nur eine kleine Frage.

Eine Parallele zu AD durch F schneidet BC in G. Also einfach eine Parallele Gerade zu AD?

---

Wie schneidet sie dann BC?

---

Da ich das nicht zeichnen kann, kann ich dir nicht weiterhelfen.