Kritische Punkte bestimmen ("Maschinenbau-Mathe")

Question

"Klassifizieren Sie die kritischen Stellen."

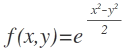
Bei der obigen Formel, weiß ich wie ich fortgehen muss, um die Nullstellen zu berechnen - x=0, y=0.  Doch bei Funktionen wie diese hier: 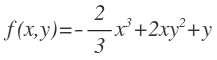hat man diese partiellen Ableitungen:

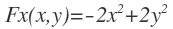
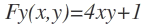. Nun weiß ich nicht wie ich die NSTn berechnen soll. Ferner rechne ich damit, dass ich mehr Nullstellen raus bekomme und weiß somit ebenfalls nicht genau, was ich mit denen anfangen soll, weil man ja nur ein x und ein y braucht, um die Extrema oder den Sattelpunkt zu klassifizieren.

Danke schonmal

Answer 1

Hallo ij,

2·y² - 2·x² = 0   ⇔ |y| = |x|   ⇔  y = x   oder y = -x

Beides einsetzen in

4·x·y + 1 = 0

  für y = x:         4x² + 1 =  0   keine Lösung

  für y = -x:    - 4x² + 1 = 0  ⇔ x² = 1/4  ⇔  x = ± 1/2

Kritische Punkte:  ( -1/2 , 1/2)  und  (1/2 , -1/2)

>"Klassifizieren Sie die kritischen Stellen." 

für jeden der 2 erhaltenen kritisichen Punkte prüfst du mit den 2. partiellen Ableitungen durch Einsetzen:

f_xx • f_yy - f_xy²    > 0 → Extrempunkt 

                         < 0  → Sattelpunkt

                         = 0     erfordert weitere Betrachtung mit Hessematrix

im Fall "Extremum" weiter:

fxx  < 0  →  Hochpunkt 

       > 0  →  Tiefpunkt

      = 0   kann nicht vorkommen

Hier kannst du dir f(x,y) anschauen:

http://www.livephysics.com/tools/mathematical-tools/online-3-d-function-grapher/?xmin=-1&xmax=1&ymin=-1&ymax=1&zmin=Auto&zmax=Auto&f=-2%2F3%2Ax%5E3%2B2%2Ax%2Ay%5E2%2By

Gruß Wolfgang