ich hoffe, ihr könnt mir helfen. Ich komm da einfach nicht weiter. Ich würde mich schon über Ergebnisse freuen, dass ich es wenigstens versuchen kann nach zu vollziehen.Ich wüsste z.b nicht wie man BC mit den vectoren a,b und c "beschreiben" soll.
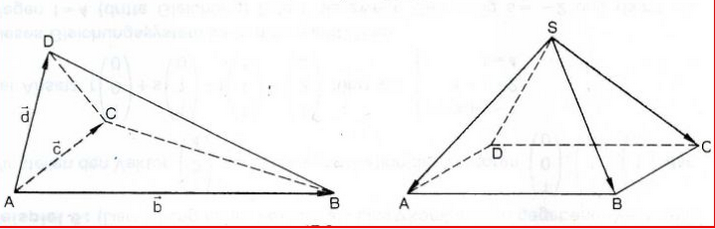
Die Vektoren \( \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{AC}} \text { und } \overrightarrow{\mathrm{d}}=\overrightarrow{\mathrm{AD}} \text { spannen eine dreiseitige Pyramide auf (Fig. } 17.3) \)
Stelle die, "Kantenvektoren" \( \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BD}}, \overrightarrow{\mathrm{CD}} \) als Linearkombination von \( \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{d}} \) dar.
Stelle die "Kantenvektoren" \( \overrightarrow{\mathrm{SD}}, \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}, \overrightarrow{\mathrm{DA}} \) der quadratischen Pyramide in Fig. 17.4 als Linearkombination der Vektoren \( \overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{SA}}, \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{SB}}, \overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{SC}} \) dar.