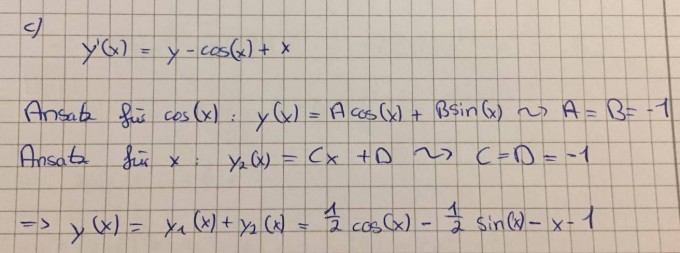Ansatz und Variation der Konstanten DGL

Question

ich verstehe die folgende Mitschrift nicht,

kann jemand erklären wie man immer auf den Ansatz kommt ?

Kann den Rechenweg nicht nachvollziehen wie man auf den Ansatz kommt oder die weiter Rechnung dann um y(x) herzuleiten...

Kann das bitte einer ausführlich erklären? :)

Answer 1

Die Ansätze kannst Du aus folg. Tabelle entnehmen: (Seite 2 . letzte Tabelle)

http://micbaum.y0w.de/uploads/LoesungsansaetzeDGLzweiterOrdnung.pdf

Du bildest dann die 1. Ableitung  (yp') , setzt diese gemeinsam mit yp in die Aufgabe ein.

Dann führst Du eine Koeffizientenvergleich durch.

Comments

Aber in der Aufgabe ist die störfunktion cos(x) und x...

Die stehen ja alleine und nicht mit Sinus oder so...

Verstehe das noch nicht wie man den Ansatz wählt, kannst du bitte eine schritt für Schritt Anleitung sagen :) wäre echt dankbar 

---

Ich habe c mit der Ansatzmethode gerechnet:

Wenn Du eine Summe als Störfunktion hast , mußt Du von beiden getrennt den Ansatz bilden und beide addieren.

---

Aber verstehe immer noch nicht wie man genau auf die Ansätze kommt...

Ich finde die Ansätze zu cos(x) in der Tabelle nicht und zu x genau so.

Es gibt da ja nur cos(x)+sin(x),

Komme nicht klar mit den Ansätzen den Rest verstehe ich aber zum Teil.

---

schau mal hier:

Seite 2

https://homepages.thm.de/~hg8070/math2kmub07/dgl_ansaetze.pdf

---

wurde bei dieser Mitschrift die ich reingestellt habe mit Variation der konstanten gerechnet ?

oder ist das ein anderes verfahren, komme gerade echt durcheinander ... :S

---

Man kann ja nicht die ganze Rechnung sehen , hier wurde es mit der Ansatzmethode gemacht.

---

das ist die komplette Rechnung... 

also ist da nichts mit Variation der konstanten ? 

---

                                                             

nein, das geht nicht so schnell.

---

                                                                                                                              

nein,

---

das ist aber die komplette Mitschrift... 

---

wie kommst du bei deiner Rechnung auf x^0 und die Zeile ??

C gehört ja zu x^1 oder nicht ?

---

mit x^0 sind die Terme verschieden von x gemeint , denn x^0 =1

---

aber wie genau kommst auf   C-D=0 

woher kommt das C ?

---

woher kommt das C ?

y_p 1 Mal abgeleitet , siehe oben