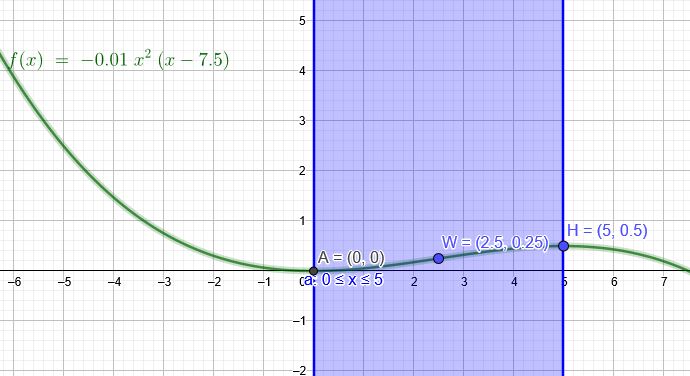
Ich lege den Punkt A in den Ursprung eines Koordinatensystem. Da die Auffahrt waagerecht beginnen soll, ist dort ein Tiefpunkt (doppelte Nullstelle)
\(f(x)=ax^2(x-N)\)
Punkt C ist ein Hochpunkt mit \(H(5|0,5)\)
\(f(5)=25a(5-N)\)
\(25a(5-N)=0,5\) → \(50a\cdot(5-N)=1\) → \(a=\frac{1}{50 \cdot (5-N)}\)
\(f(x)=\frac{1}{50 \cdot (5-N)}x^2(x-N)\)
Bei einer kubischen Parabel liegt der Wendepunkt ( Punktsymmetrie) immer in der Mitte zwischen Tiefpunkt\(T(0|0)\) und Hochpunkt \(H(5|0,5)\) → \(W(2,5|0,25)\)
\(f(2,5)=\frac{1}{50 \cdot (5-N)} \cdot 6,25 \cdot (2,5-N)\)
\(\frac{1}{50 \cdot (5-N)} \cdot 6,25 \cdot (2,5-N)=0,25\)
\(N≈7,5\) \(a≈\frac{1}{50 \cdot (5-7,5)}=-0,008\)
\(f(x)≈-0,008x^2(x-7,5)\)