Wie Definitionsbereich einer verketteten Funktion bestimmen

Question

Könnt ihr mir bitte helfen , ich komme bei der Aufgabe einfach nicht weiter...

Answer 1

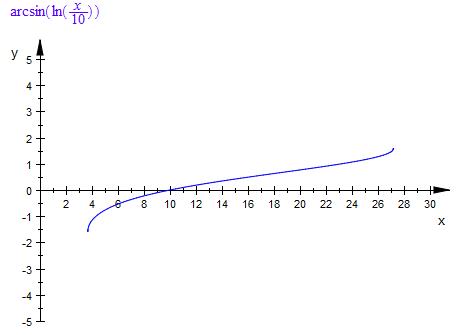
Die arcsin Funktion ist bildlich die
sin-Funktion um 90 ° gedreht,
x- und y-achse sind vertauscht.

https://de.wikipedia.org/wiki/Arkussinus_und_Arkuskosinus

Der Def-Bereich geht von -1 bis 1.

Da es dann zu jedem x-Wert unendlich
viele y-Werte gibt ist der Wertebereich auf
- π / 2 bis π / 2 eingeschränkt.

D = -1 .. 1

ln ( x / 10 ) darf nur Werte im Def-Bereich
annehmen.
ln ( x / 10 ) = -1
x / 10 = e ^{-1}
x = 10 / e ^1

ln ( x  / 10 ) = 1
x / 10 = e ^1
x = e * 10

Die beiden Werte liegen im Def-Bereich
einer ln - Funktion.

f ( x ) = arcsin ( ln ( x / 10) )
D = [ 10 / e ; 10 * e ]
W = [ - π / 2 ; π / 2  ]

Comments

f ( x ) = arcsin ( ln ( x / 10) )
D = [ 10 / e ; 10 * e ]
W = [ - π / 2 ; π / 2  ]

Umkehrfunktion
x =  arcsin ( ln ( y / 10) )
sin ( x ) = ln ( y / 10 ) | e ()
e ^{sin [x]} ) = y / 10
y = 10 * e ^{sin[x}}

Def- und Wertebereich sind bei der
Umkehrfunktion vertauscht
f ^{-} ( x )  = 10 * e ^{sin[x}}
D = [ - π / 2 ; π / 2  ]
W = [ 10 / e ; 10 * e ]

y0 = f ( x0 )
Liegt y0 im Def - Bereich von
f  ^{-} gibt es eine eindeutige
Lösung. Siehe den Graph.

---

vielen Dank für deinen Beitrag, aber gibt es nicht eine eindeutige Lösung?

---

Was genau verstehst du nicht ?

Gebe gern Auskunft bis alles geklärt ist.