Hallo,
Könnt ihr mir bitte helfen.
dazu müsste man genau wissen, bei was Du ein Verständnisproblem hat. Du fragst:
Wie kommt man auf diese x,y Ebenengleichung, wenn es doch kein s gibt?
Die Parameterform einer Ebene hat immer zwei Variablen, die oft mit \(s\) und \(t\) bezeichnet werden. Die allgemeine Parameterform ist$$E: \quad \vec x = \vec p + \vec u s + \vec v t$$bzw. in Deinem Fall:$$E: \quad \vec x = \begin{pmatrix}1+s-2t\\ s\\ t\end{pmatrix} = \begin{pmatrix}1\\ 0\\ 0\end{pmatrix}+ \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}s + \begin{pmatrix}-2\\ 0\\ 1\end{pmatrix} t $$
Wie kommt man auf diese x,y Ebenengleichung, ...
es geht doch nur darum, drei Vektoren \(\vec p\), \(\vec u\) und \(\vec v\) zu bestimmen, die die Parameterform für die Ebene bilden. Wobei zu beachten ist, dass die Lösung nie eindeutig ist.
Die Koordinatenform der Ebene ist gegeben:$$E: \quad x-y+2z=1 \quad \text{bzw.} \quad \begin{pmatrix}1\\ -1\\ 2\end{pmatrix} \vec x = 1$$Um einen Vektor \(\vec p\) zu bestimmen, reicht es aus, irgendeine Lösung dieser Gleichung zu kennen.
In der Aufgabe steht '\(y\) und \(z\) als Parameter'. Setze also z.B. \(y=z=0\), dann bleibt \(x=1\), um die Gleichung zu erfüllen. Also ist ein mögliches \(\vec p\)$$\vec p = \begin{pmatrix}x=1\\ y=0\\ z=0\end{pmatrix} = \begin{pmatrix}1\\ 0\\ 0\end{pmatrix}$$Genauso gut hätte man aber auch $$\vec p_2 = \begin{pmatrix}0\\ -1\\ 0\end{pmatrix} \quad \text{oder} \quad \vec p_3 = \begin{pmatrix}0\\ 1\\ 1\end{pmatrix}$$nehmen können. Wie schon geschrieben: die Paramerform ist nie eindeutig.
Für den ersten Richtungsvektor \(\vec u\) setze nun die Y-Koordinate zu \(0\) und die Frage ist, wie \(x\) und \(z\) aussehen müssen, damit die Koordinatengleichung immer \(0\) ergibt (und nicht \(1\)!). Eine bewährte Methode ist es, die beiden verbleibenden Koordinaten zu vertauschen und eine der beiden zu negieren. So wird aus$$\begin{pmatrix}1\\ -1\\ 2\end{pmatrix} \to \begin{pmatrix}1\\ y=0\\ 2\end{pmatrix} \to \vec u = \begin{pmatrix}-2\\ 0\\ 1\end{pmatrix}$$wenn man diese beiden Werte mit einem beliebigen Faktor multipliziert (mit \(s\)) und in die Kordinatenform einsetzt, so kommt immer \(0\) heraus. Da das \(\vec p\) ja bereits die \(1\) liefert, erfüllt die Summe aus beiden immer die Koordinatengleichung.
Und auf die selbe Weise kommt man zu Vektor \(\vec v\): $$\begin{pmatrix}1\\ -1\\ 2\end{pmatrix} \to \begin{pmatrix}1\\ -1\\ z=0 \end{pmatrix} \to \vec v = \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}$$
Bei all dem ist außerordentlich hilfreich, sich das ganze auch räumlich vorzustellen. Hier sieht das so aus:
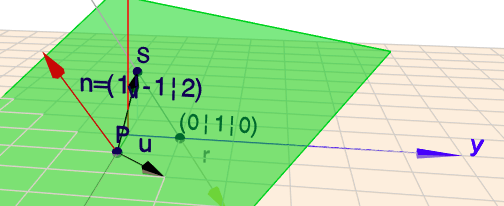
klick auf das Bild, dann öffnet sich die Szene in Geoknecht3D und Du bekommst einen besseren räumlichen Eindruck.
Und zu der orthogonalen Zerlegung: Ist es immer so , dass man bei der Zerlegung des Richtungsvektor, die Anzahl Ebenen beim Nenne drauf packt?(3*Wurzel(6))
Es ist nur eine Ebene vorhanden, und die ist auch nicht relevant. Es gilt, den Einheitsnormalenvektor der Ebene \(\hat n\) in zwei Komponenten zu zerlegen. Ich habe das mal versucht darzustellen:
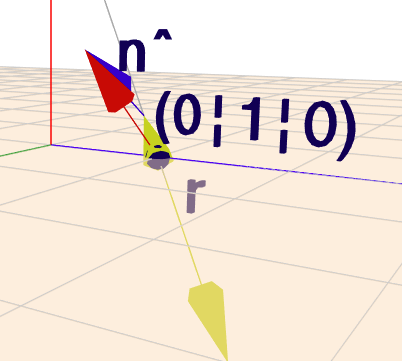
Der rote Vektor \(\hat n\) soll in zwei Komponenten zerlegt werden. De erste ist \(\hat n_{\parallel}\) (gelb), d.h. die verläuft in Richtung des Richtungsvektors der Geraden, und die zweite Komponente \(\hat n_{\perp}\) (blau) steht senkrecht auf eben diesem Richtungsvektor. Die Summe von beiden Komponenten ist wieder \(\hat n\)$$\hat n = \hat n_{\parallel} + \hat n_{\perp}$$
Wie geht man da genau vor, dass n|= ((-2)/3√6) UND n|_ = 1/(3√6) rauskommt?
Um einen beliebigen Vektor \(\vec c\) orthogonal in zwei Komponenten \(\vec c_{\parallel}\) und \(\vec c_{\perp}\) zu zerlegen, von denen die eine in Richtung \(\vec r\) verläuft, geht man wie folgt vor. Es ist$$\vec c_{\parallel} = \frac{ \vec c \cdot \vec r }{\vec r^2} \vec r, \quad \vec c_{\perp} = \vec c - \vec c_{\parallel} $$wobei \(\vec c \cdot \vec r \) das Skalarprodukt ist. Hier ist $$\vec c = \hat n = \frac 1{\sqrt 6} \begin{pmatrix}1\\ -1\\ 2\end{pmatrix}, \quad \vec r = \begin{pmatrix}1\\ 1\\ -1\end{pmatrix} \implies \vec r^2 = 3$$... rechne es selber nach.
Zu dem Rest der Aufgabe stelle bitte konkrete Fragen, wenn Du irgendwas nicht verstanden hast.