Ableitung Funktionen tangente

Question

Gegeben sei die Funktion x³+ y³=3axy

Für welches a hat der Graph der Funktion eine horizontale Tangente im Punkt P (4;2) 

Danke 

Comments

Sicher, dass du 

" Für welches a hat der Graph der Funktion eine horizontale Tangente im Punkt P (4;2) ? " exakt wiedergegeben hast? 

"im Punkt P" bedeutet, dass schon die Kurve durch den Punkt P geht. 

Steht da vielleicht:

"Für welches a hat der Graph der Funktion eine horizontale Tangente, die durch den Punkt P (4;2) geht? "

Das wäre etwas völlig anderes. 

Answer 1

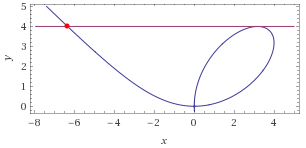
Sollte die Funktion durch den Punkt $(2;4)$ gehen, dann ist $a=3$, wie Roland schon ausgeführt hat. In diesem Punkt hat die Funktion aber keine waagerechte Tangente. Die Steigung bestimmt man, indem man die Funktion ableitetet.

Georg schrieb: "Man müßte die Gleichung als y ( x ) = ...  schreiben."

Muss man nicht - einfach nach $x$ ableiten gibt:

$$3x^2 + 3y^2\cdot y' = 3a(y + x\cdot y')$$

Umstellen nach $y'$ und man erhält:

$$y'=\frac{ay-x^2}{y^2-ax}$$

Eine horizontale Tangente - d.h. $y'=0$ - liegt an der Position:

$$ay - x^2=0 \quad \Rightarrow x=\sqrt{ay}$$

Lautet die Aufgabe also "Für welches a hat der Graph der Funktion eine horizontale Tangente, die durch den Punkt P (4;2) geht? " dann muss hier nur $y=4$ sein. Zusätzlich muss das Paar $(x;y)$ natürlich ein Punkt der Funktion sein. Demzufolge ist nach Einsetzen von $x=\sqrt{ay}$ in die ursprüngliche Funktion

$$ay\sqrt{ay} + y^3 = 3a\sqrt{ay} \cdot y$$

Auflösen nach $a\sqrt{a}$ und Einsetzen von $y=4$ gibt

$$a\sqrt{a} = a^{\frac32}=4 \quad \Rightarrow a = 4^{\frac23} \approx 2,52$$

Comments

Diese Funktion nennt man 'Kartesisches Blatt'.

---

Meinen Glückwunsch Werner.
Für mich ist die Antwort zu hoch. Grins.

---

Der Vollständigkeit halber sollte man  vielleicht erwähnen, dass es keine Funktion ist.

---

Für mich ist die Antwort zu hoch.

Öh - das hätte ich nicht gedacht. Was genau an meiner Antwort verstehst Du nicht? Wo muss ich die Antwort noch mehr ausführen?

---

x³+ y³=3axy

- einfach nach x ableiten gibt:

3x² + 3y² * y´ = 3a ( y + x * y´ )

wie kommt man von y³ auf 3y² * y´

Ein Literatur / Internethinweis könnte auch
genügen.

---

Du kennst die Regel - es ist die Kettenregel.

$y=f(x)$ und wenn man den Term $f(x)^3$ nach $x$ ableitet, so erhält man $3f(x)^2 \cdot f'(x)=3y^2\cdot y'$.

Answer 2

x³+ y³=3axy
für x = 4 und y = 2 ist a = 12

x³+ y³=3*12*xy
x³+ y³ = 36*xy
y³ - 36y = - x³

Wie´weitergehen soll weiß ich leider nicht.

Man müßte die Gleichung als
y ( x ) = ...
schreiben. Die erste Ableitung bilden
und dann nachschauen ob bei x = 4
die Steigung 0 ist.

Comments

Hallo Georg, du schreibst
für x = 4 und y = 2 ist a = 12

müsste es nicht heißen
für x = 4 und y = 2 ist a = 3 ?

---

Morgen Roland, richtig.
Die Quizfrage bleibt aber.
Wie geht es weiter ?
y³ - 12y = - x³
Wie kann die Frage beantwortet werden ?

---

Morgen Roland, richtig.
Die Quizfrage bleibt aber.
Wie geht es weiter ?
y³ - 12y = - x³
Sollte man eine Wertetabelle berechnen und dann
den Graph zeichnen ?

---

"Man müßte die Gleichung als
y ( x ) = ..."

Vorschlag:

x(y) müsste in y = 2 eine nicht definierte Steigung haben. Das scheint aber nicht zu stimmen (oder? Da ist ja eine Wurzel dabei)

---

Ich meine auch wir sollten erst einmal
klären wie die Aufgabe wirklich lautet.

@Fragesteller : Originalfragetext oder
Foto desselben einstellen

---

Guten Morgen Georg,

ich hab die gegebene Gleichung x³+y³=9xy von meinem CAS nach y auflösen lassen. Da kam ein grausiger Term heraus. Die Ableitung war noch grausiger und die Nullstelle der Ableitung hat mein CAS nach 30 min Rechenzeit nicht gefunden.

---

Die Fragestellung ist schon unsinnig
Ich warte erst einmal ab.

---

So geht das:

https://de.m.wikipedia.org/wiki/Implizite_Differentiation