Orthogonalbasis, orthogonale Projektion auf eine Ebene

Question

ich brauche Hilfe bei der folgenden Aufgabe:

Aufgabenteil a): Ergänzen sie die beiden Vektoren zu einer orthonormalbasis.

 

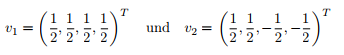
Meine Überlegung war, entweder die Einheitsvektoren von R^4 zu nehmen, bzw. so im Nachhinein (1,-1,0,0) und (0,0,1,-1) zu verwenden.

Aufgabenteil b): Es sei E = Lin(v1, v2) die von v1 und v2 aufgespannte Ebene. Bestimmen Sie
für x ∈ R4 den Bildvektor π_E(x) unter der orthogonalen Projektion auf E. 

Es gilt ja π_E(x) = ∑ i=1 bis n  < x_{i ,} v >, jedoch weiß ich hier noch nicht wie ich hier weiter machen soll.

Comments

Vom Duplikat:

Titel: Bildvektor unter der orthogonalen Projektion

Stichworte: projektion,gerade,orthogonal

Hallo mein Problem ist bei Teil (b) , bei (a) würde ich einfach Gram-Schmidt benutzen aber bei (b) habe ich keine Ahnung.

Answer 1

Die beiden bilden mit (1,-1,0,0)^T und (o,o,1,-1)^T eine

orthogonale Basis von R4.  Also musst du sie nur noch

normieren.

Zu 2) Deine Formel ist falsch.

Das Ergebnis wäre ja eine Zahl, muss aber ein Vektor sein.

Comments

Die ganze Basis normieren? Sprich v1, v2, v3, v4? Und wie genau soll ich mir das vorstellen (Die Formulierung verwirrt mich)? u1 = 1/||v1|| * v1? Also Gram-Schmidt Verfahren?

Ja stimmt, hast du recht, dann hab ich sie wohl im falschen Zusammenhang aufgeschnappt.

Kannst du mir dann eventuell auf die Sprünge helfen, wie ich sonst vorgehen kann/soll?

---

gram-schmidt brauchst du nicht vollständig.

Nur normieren, also für jeden der 4

Basisvektoren vi einfach 

ui = 1/||vi|| * vi?

---

Und was bringt das normieren? 

v1 normiert= (1,1,1,1)

v2= (1/2,1/2,-1/2,-1/2)

v3 normiert ergibt (-1/√2,1/√2,0,0)

...

Was hab ich nun davon? Welche Erkenntnis kann man daraus ziehen?

---

v1 normiert= (1,1,1,1)

ist falsch, der hat ||v1|| = 2 (und nicht 1)

v1 , v2 waren schon normiert !

Was hab ich nun davon? 

Hier hast du erst mal nur die Lösung der Aufgabe.

Allgemein liegt der Sinn wohl eher darin:

https://de.wikipedia.org/wiki/Orthonormalbasis#Orthogonale_Abbildungen

---

Also reicht als Lösung nur, v3 und v4 normieren? 

Muss man nicht zusätzlich zeigen, wie man auf die beiden vektoren gekommen ist? Beweisen, dass die linear unabhängig sind? Und dass die Skalarprodukte =0 sind? 

---

Muss man nicht zusätzlich zeigen, wie man auf die beiden vektoren gekommen ist?

Nein

Beweisen, dass die linear unabhängig sind?   Ja

Und dass die Skalarprodukte =0 sind?  Ja

---

 

Muss ich die Skalarprodukte einmal für alle möglichen Kombinationen durchgehen? 

Sprich <v1,v2>, <v2,v3>, <v1,v4>,...

---

Ja, ich bin auch jede einzelne Kombination durchgegangen, da ja gilt:

< vi , vj > = 0 für i ≠ j.

Aber auch vielen Dank, für die Antworten!

Jedoch wird mir die b) immer noch nicht ganz klar.

---

Also muss man bei (a) nur (1,-1,0,0) und (0,0,1,-1) normieren und somit  (v1,v2,1/sqrt(2)* (1,-1,0,0),1/sqrt(2)*(0,0,1,-1)) bilden eine Orthonormalbasis ? 

---

Das ist wohl richtig.

---

Eine frage, warum habt ihr oben  v3=(1,-1,0,0) und v4=(0,0,1,-1) genommen , wäre es nicht leichter mit v3=(1,0,0,0) und v4=(0,0,0,1) ?

---

Die wären nicht orthogonal zu v1 und v2.

---

Aber wie bestimme ich den Bildvektor π E(x) im Aufgabenteil b)?

---

v3 und v4 sind aber auch ohne Normierung orthogonal und bilden somit eine Basis. Ist das normieren dann nicht überflüssig?

---

Nein, da in der Aufgabe nach der Orthonormalbasis gefragt wird und dies beinhaltet die Normierung.

---

Prüfe ich die orthogonalität und lineare Abhängigkeit nun mit v3 und v4 oder erst mit den normierten Vektoren? 

---

Wie bist du eigentlich auf  (1,-1,0,0)T und (o,o,1,-1)T gekommen ? ist das Standard für R^4 ?

---

Das Skalarprodukt muss ja = 0 sein, also hab ich geschaut wie das passt: 

1/2 * 1 + 1/2 * (-1) + 1/2 * 0 + 1/2 * 0 = 0

1/2 * 0 + 1/2 * 0 + (-1/2) * (-1) + (-1/2) * 1 = 0