Hallo KurodaAkira,
ln(1+x) - ln(x) = ln( (1+x) / x ) = ln( 1 + 1/x) ; D = ℝ+
f: ℝ+ → ℝ+ ; x ↦ ln( (1+x) / x ) [# vgl. unten]
y = ln( (1+x) / x )
nach x auflösen:
ey = (1+x)/x
x*ey = 1+x
x*ey - x = 1
x * ( ey - 1 ) = 1 | : ( ey - 1 ) ; ≠ 0 wegen y∈ℝ+
x = 1 / ( ey - 1 )
Variablennamen vertauschen
y = 1 / ( ex - 1 )
f -1 : ℝ+ → ℝ+ , x ↦ 1 / ( ex - 1 )
Der Graph von f -1 ergibt sich aus dem von f durch Spiegelung an der 1. Winkelhalbierenden:
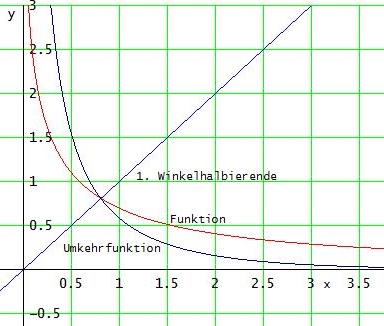
#
f '(x) = [ ln(1+x) - ln(x) ] ' = 1/(x+1) - 1/x < 0 für x∈ℝ+
→ f ist streng monoton fallend
limx→0+ f(x) = limx→0+ ln( 1 + 1/x) = ∞ ; limx→∞ f(x) = 0+
Die Bildmenge von f ist also ℝ+
Gruß Wolfgang