Polynomfunktion aufsuchen

Question

Eine Funktion dritten grades hat den Hochpunkt H(1/5) und den Wendepunkt W(2/3)

Answer 1

Ansatz:

f(x)=Ax^3+Bx^2+Cx+d

Gleichungen

f(1)=5

f(2)=3

f'(1)=0

f''(2)=0

setzte ein und löse das Gleichungssystem.

Comments

Achsoo dann muss ich einfach bei jedem dieser Beispiele einsetzen und lösen. Ahh. Dankee

---

Genau ! :)      fülllllllltext        

Answer 2

Ansatz: f(x)=ax³+bx²+cx+d; f '(x)=3ax²+2bx+c; f ''(x)=6ax+2b
Hochpunkt H(1/5) führt zu (1) 5=a+b+c+d und (2) 0=3a+2b+c

 Wendepunkt W(2/3) führt zu (3) 3=8a+4b+2c+d und (4) 0=12a+2b

Das sind vier Gleichungen mit vier Unbekannten, von denen ich hoffe, dass du sie lösen kannst.

Answer 3

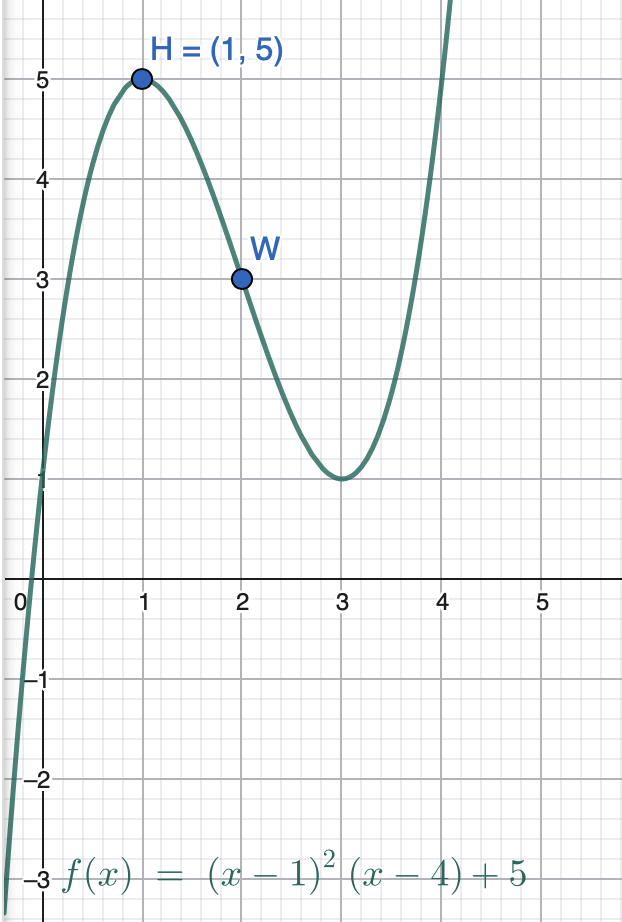
Eine Funktion dritten Grades hat den Hochpunkt H(1|5) und den Wendepunkt W(2|3)

Verschiebung um 5 Einheiten nach unten: H(1|5)  →   H´(1|0) An der Stelle x=1 ist eine doppelte Nullstelle: Linearfaktorenform

\( f(x)=a(x-1)^2(x-N)]\\=a(x^2-2x+1)(x-N)\\=a(x^3-Nx^2-2x^2+2Nx+x-N)\)   Wendepunkt 2. Ableitung

\( f'(x)=a(3x^2-2Nx-4x+2N+1)\)

\( f''(x)=a(6x-2N-4)\).

\( f''(2)=a(12-2N-4)=a(8-2N)=0\)

\(N=4 \).

\( f(x)=a(x-1)^2(x-4) \)

W(2|3)  →W´(2|-2)\( f(2)=a[(2-1)^2(2-4)] =-2a=-2\)        \( a=1\).

\( f(x)=(x-1)^2(x-4) \)    Verschiebung um 5 Einheiten nach oben:  

\( p(x)=(x-1)^2(x-4)+5\)