Polynomfunktion dritten Grades suchen

Question

Eine Parabel 3. Ordnung schneidet die x-Achse bei x=1 hat im punkt E(-2/3)ein Extremum und bei x=0 einen Wendepunkt.

Answer 1

Ansatz: f(x)=ax³+bx²+cx+d; f '(x)=3ax²+2bx+c; f ''(x)=6ax+2b

schneidet die x-Achse bei x=1 führt zu (1) 0=a+b+c+d

hat im punkt E(-2/3) ein Extremum führt zu (2) 3=-8a+4b-2c+d und (3) 0=12a-4b+c

bei x=0 einen Wendepunkt. führt zu (4) 0=2b

Das sind vier Gleichungen mit vier Unbekannten, von denen ich hoffe, dass du sie lösen kannst.

Answer 2

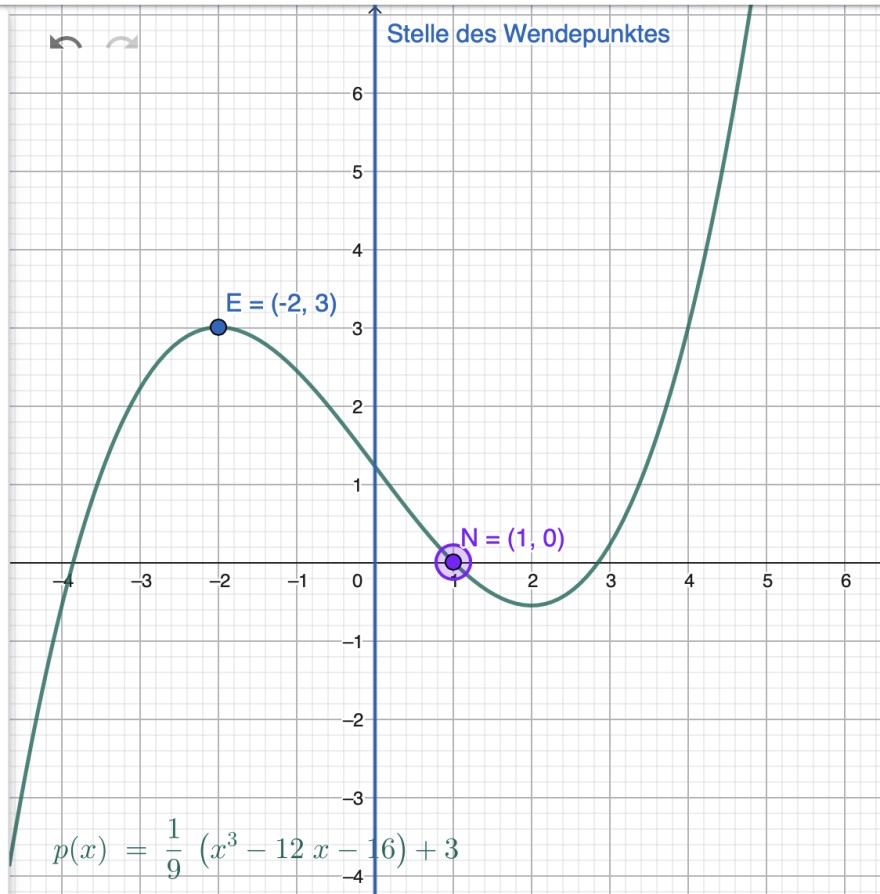
Eine Parabel 3. Ordnung schneidet die x-Achse bei x=1 hat im Punkt E(-2|3)ein Extremum und bei x=0 einen Wendepunkt

...hat im Punkt E(-2|3)ein Extremum. Verschiebung um 3 Einheiten nach unten. E´(-2|0)  An der Stelle  x=-2 ist eine doppelte Nullstelle

Linearfaktorenform:

\( f(x)=a(x+2)^2(x-N)=a(x^2+4x+4)(x-N)=a(x^3-Nx^2+4x^2-4Nx+4x-4N) \)

...und bei x=0 einen Wendepunkt 2. Ableitung

\( f'(x)=a(3x^2-2Nx+8x-4N+4) \).

\( f''(x)=a(6x-2N+8) \)

\( f''(0)=a(-2N+8)=0 \)    →      \(N=4 \)→ \( f(x)=a(x^3-12x-16) \)

N(1|0)→N´(1|-3)    →  \( f(1)=a(1-12-16)=-27a=-3 \)     → \( a=\frac{1}{9} \)→ \( f(x)=\frac{1}{9}(x^3-12x-16) \)

...und um  3 Einheiten nach oben:   \( p(x)=\frac{1}{9}(x^3-12x-16)+3 \)

Answer 3

Eine Parabel 3. Ordnung schneidet die x-Achse bei x=1 hat im punkt E(-2/3)ein Extremum und bei x=0 einen Wendepunkt.

Verwende https://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle.

Eigenschaften

f(1) = 0
f(-2) = 3
f'(-2) = 0
f''(0) = 0

Gleichungssystem

a + b + c + d = 0
-8a + 4b - 2c + d = 3
12a - 4b + c = 0
2b = 0

Funktion

f(x) = 1/9·x^3 - 4/3·x + 11/9