Hallo Om,
um die Geradengleichung zu ermitteln, wenn zwei Punkte gegeben sind, berechnest du zuerst die Steigung m:
$$ m=\frac{y_2-y_1}{x_2-x_1} $$
Den Schnittpunkt mit der y-Achsel musst du in diesem Fall nicht berechnen, da bekannt = Ursprung.
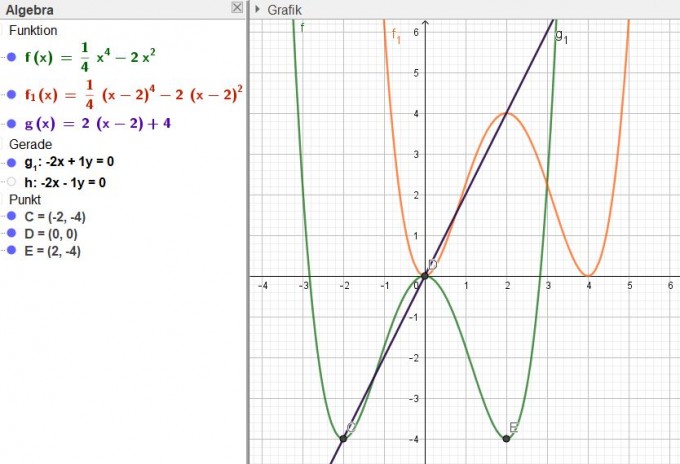
Also g(x) = 2x
(Was ist mit der Gerade durch T2 und h? Solltet ihr diese Gerade auch bestimmen?)
Damit der Punkt T1 im Ursprung liegt, muss der Graph um zwei Einheiten nach rechts (x-2 für x einsetzen) und um 4 Einheiten nach oben verschoben werden (+4 "hinzufügen")
Somit lautet der neue Funktionsterm
$$ f_1(x)=\frac{1}{4}(x-2)^4-2(x-2)^2+4 $$
Die Gleichung der Geraden wird ebenso verändert:
g(x) = 2(x-2) + 4
= 2x - 4 + 4
= 2x
Gruß, Silvia