Wie löse ich diese Gleichung? 0,0016x^3+0,0048x^2-0,072=0

Question

Ich wollte wissen, wie die folgende Gleichung zu lösen ist:

0,0016x^3+0,0048x^2-0,072=0

Danke schonmal für die Hilfe!

LG

Comments

Ersetze * durch ^ falls du hoch meinst.

* ist mal.

Nachtrag: Habe das oben zu ^  korrigiert.

---

Tut mir Leid, ich meinte natürlich:

0,0016x^3+0,0048x^2-0,072=0

---

0,0016x^3+0,0048x^2-0,072=0
Mir wäre es lieber es würde
0,0016x^3+0,0048x^2-0,072 * x =0
heißen.
Stell einmal ein Foto der Aufgabe ein.

---

Würde es so heißen wie bei Georg, dann könnte man den Satz vom Nullprodukt anwenden!

Answer 1

0.0016·x^3 + 0.0048·x^2 - 0.072 = 0

x^3 + 3·x^2 - 45 = 0

Wertetabelle liefert eine Lösung zwischen 2 und 3. Ein Näherungsverfahren deiner Wahl liefert x = 2.788.

Answer 2

Multipliziere mit 625 und erhalte \(x^3+3x^2-45=0\).
Substituiere \(x=\frac u3+\frac3u-1\) und erhalte \((2u^3-1161)^2=1345005\).
Berechne daraus \(u\) und resubstituiere.

Comments

Zu lösen sei \(x^3+ax^2+bx+c=0\).
Substitution: \(x=\dfrac{u-a}3+\dfrac{a^2-3b}{3u}\).
Ergebnis: \(u^6+(2a^3-9ab+27c)u^3+(a^2-3b)^3=0\).
Viel Spaß beim Nachrechnen!

Answer 3

Nach dem Newton-Verfahren gilt:$${x}_{1}={x}_{i}-\frac{f{x}_{i}}{f'{x}_{i}}$$Du musst nun also die erste Ableitung bilden:$$f'(x)=\dfrac{3x\left(x+2\right)}{625}$$Du musst nun einen guten Startwert finden, ich würde die 3 nehmen.$${x}_{1}=3-\frac{f(3)}{f'(3)}$$ Konkret heißt das:$${x}_{1}=3-\frac{0,0016\cdot 3^3+0,0048\cdot 3^2-0,072}{\left(\dfrac{3\cdot 3\left(3+2\right)}{625}\right)}= 2.8$$ Du musst diesen neuen Wert (2.8) nun wieder in die Formel einsetzen, bis sich kaum noch was ändert oder die gewünschte Präzision erreicht ist:$${x}_{2}={x}_{1}-\frac{f({x}_{1})}{f'({x}_{1})}$$

Du musst das ganze 5 Mal machen, wenn du die Präzision einer Rechenmaschine erreichen möchtest

Answer 4

Du schreibst leider weder was zu:

- Klassenstufe?

- Wissensstand von?

- gewünschte Genauigkeit?

So können wir an dieser Aufgabe die 1000 Jahre Geschichte der Mathematik aufschreiben...

a) Untere Klassen tasten sich - wie vor 700 Jahren - durch Probieren (oder grafische Zeichnen & Ablesen) heran.

Bei Wikipedia ist das Bisektion und per http://www.gerdlamprecht.de/Roemisch_JAVA.htm

Beispiel 2 hat man im Suchbereich von 1...4 nach 38 Schritten mehr als 13 Stellen genau:

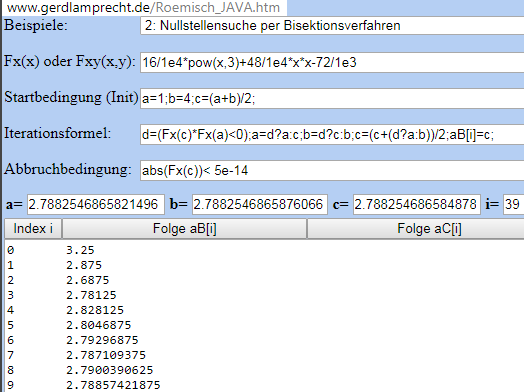
Ob man 16/1e4 oder 0.0016 schreibt ist egal.

b) So 1680 herum (oder Klassenstufe 9 aufwärts) erkannten schlaue Leute, dass eine Iteration mit der Ableitung schneller als die Bisektion ist und statt 2 Suchwerte nur 1 Startwert nötig ist:

Unter Wiki https://de.wikipedia.org/wiki/Newton-Verfahren und http://www.gerdlamprecht.de/Roemisch_JAVA.htm

rechnet das im Beispiel 118 online vor. Ob man dabei symbolisch oder numerisch ableitet ist egal:

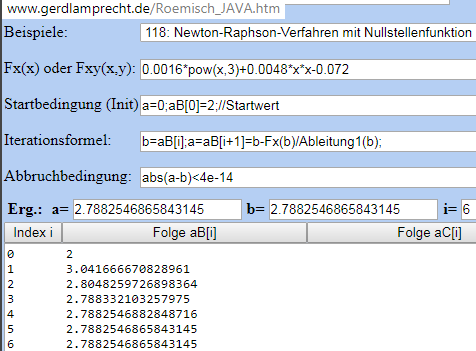
Bei Startwert 2 ist man schon nach 6 Schritten mehr als 13 Stellen genau.

c) Im 16. Jh. fand man exakte https://de.wikipedia.org/wiki/Cardanische_Formeln

die aber noch Fallunterscheidungen und viele trigonometrische Funktionen hatten.

d) Dann gibt es sehr begabte wie nn (siehe seine Antwort), die eine sehr komplizierte Spezialfall-Substitution sehen (oder von WolframAlpha . com abschreiben)

e) Der aktuelle Wissensstand (Uni) sind jedoch fertige explizite PQRST-Formeln, die man analog zur pq-Formel einfach nur einsetzen muss: Der Nullstellenrechner rechnet c) und e) online vor

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

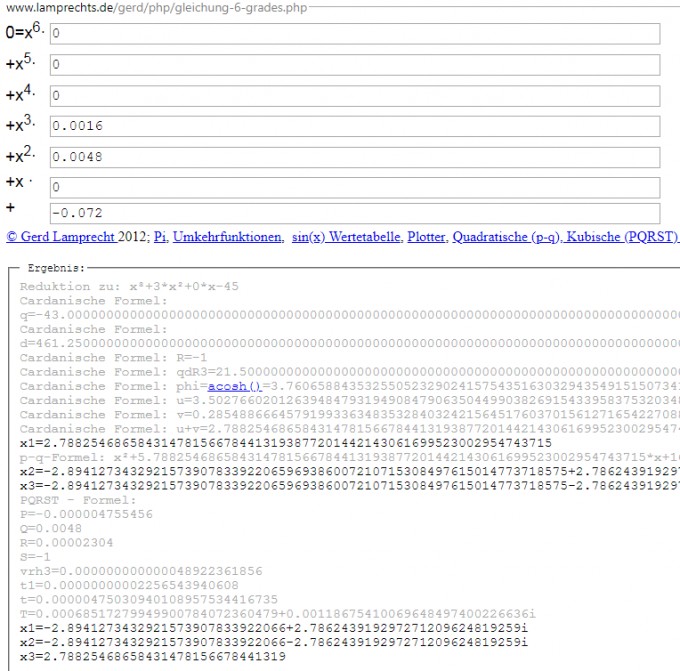
Dort auch der LINK zur PQRST-Formel http://www.lamprechts.de/gerd/Quartische_Gleichung.html

die immer 3 Lösungen hat, die auch komplex oder übereinanderliegend sein können.

Mit expliziten Formeln lautet das einzige NICHT-komplexe Ergebnis

x3 = ((43 - 3*sqrt(205))/2)^{1/3} + ((43 + 3*sqrt(205))/2)^{1/3}-1 mit sqrt(x)=x^{1/2}=Wurzel(x)

Will man mehr als 10000 Nachkommastellen berechnen, ist das mehrfache Wurzelziehen (welches auch wieder iterativ erfolgt) langsamer als die Newton-Iteration.