Aufgabe:
Ein Institut untersucht die Reisedauer von Urlaubsreisen in Abhängigkeit von der Entfernung vom Wohnort der Urlauber. Es gehen nur Innländische Urlaubsreisen in die Statistik ein. Aus der Urliste liegen das Streudiagramm Reiseweite vs. Reisedauer, eine Klasseneinteilung sowie die resultierende Kreuztabelle zur Auswertung vor:
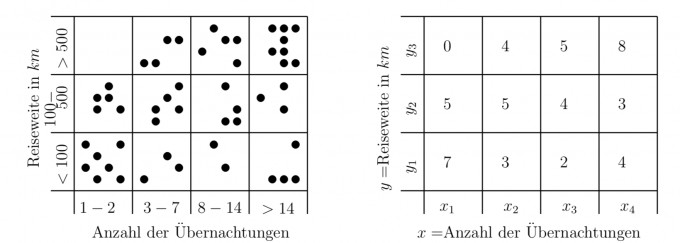
(a) Die relativen Häufigkeiten h(xi,yj),
(b) die Randhäufigkeiten A(xi) bezüglich Merkmal Anzahl der Übernachtungen sowie A(yj) bezüglichMerkmal Reiselänge sowie die relativen Randhäufigkeiten h(xi) und h(yj),
(c) die Verteilungsfunktionen der Randhäufigkeiten,
(d) die bedingten relativen Häufigkeiten sowie die Verteilung der Reiselängefür 1 − 2 und
> 14 Übernachtungen,
(e) die Übernachtungszahl-Verteilung der Urlauber mit Reiselänge unter 100 km,
(f) die durchschnittliche Reiseweite der Urlauber mit 1-2, 3-7, 8-14 und >14 Übernachtungen,