2 Punkte auf e-Funktion verbinden: Mittelwert (Beweis)?

Question

Hallo. Wenn man zwei Punkte einer E Funktion miteinander verbindet und den Mittelwert M(x1/y1) einzeichnet, so ist der Funktionswert der E Funktion an der Stelle x1 immer größer als y1!

Wer kann dies mathematisch beweisen?

Comments

Meinst du die Funktion

f(x) = e^x als E-Funktion

Dort ist doch aber der Mittelwert zweier Punkte immer größer als der Funktionswert in der Mitte der beiden Punkte oder nicht ?

---

f(x) = e^x ist streng konvex gekrümmt. Alle Sekanten über so einer Funktion liegen oberhalb der Funktionskurve. Mir ist halt nicht klar, von welchem Mittelwert (Sekante oder Funktion) hier die Rede ist.

Answer 1

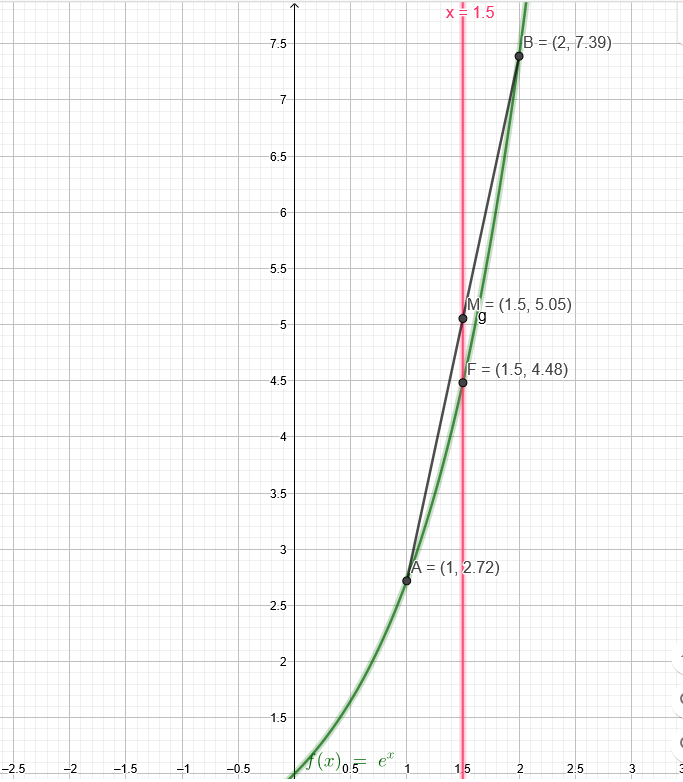
Ich stelle mal das Bild dazu ein . Es ist nicht mit Latex geschrieben, weil dies für mich zu kompliziert wäre.

Es muss heißen, dass der Funktionswert kleiner ist.  

Bitte runterscrollen!

Text erkannt:

Es muss heißen: Der Funktionswert ist kleiner. $A\left(a \mid e^{a}\right)$ und $B\left(b \mid e^{b}\right)$ mit $a<b$
$M\left(\frac{a+b}{2} \mid \frac{e^{a}+e^{b}}{2}\right)$
$f\left(\frac{a+b}{2} \mid e^{\frac{a+b}{2}}\right)$
$e^{\frac{a+b}{2}}<\frac{e^{a}+e^{b}}{2}$
$e^{\left(\frac{a}{2}+\frac{b}{2}\right)}<\frac{e^{a}+e^{b}}{2}$
$e^{\frac{a}{2}} \cdot e^{\frac{b}{2}}<\frac{e^{a}+e^{b}}{2} \mid \cdot 2$
$2 \cdot e^{\frac{a}{2}} \cdot e^{\frac{b}{2}}<e^{a}+e^{b}$
$0<e^{a}-2 \cdot e^{\frac{a}{2}} \cdot e^{\frac{b}{2}}+e^{b}$
Substitution:
$e^{a}=u \rightarrow a=\ln u$
$e^{b}=v \rightarrow b=\ln v$
$0<u-2 \cdot \sqrt{u} \cdot \sqrt{v}+v$
$2 \cdot \sqrt{u \cdot v}<u+\left.v\right|^{2}$
$0<u^{2}-2 u v+v^{2}$
$0<(u-v)^{2}$
Rücksubstitution:
$0<\left(e^{a}-e^{b}\right)^{2}$
$q \cdot e \cdot d$
$\mathrm{mfG}$
Moliets