(i) 1.-2.Ableitung bilden -> Die brauchst du gleich
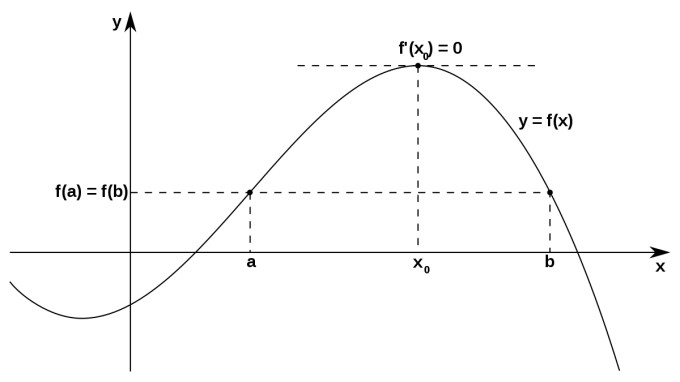
(ii) Notwendige Bedingung: f'(x)=0
Du musst die erste Ableitung gleich 0 setzen, weil du diejenige Stelle(n) suchst, an der/denen die Steigung gleich 0 ist. Man kann sich das gut an einem Berg anschauen: Ganz oben an der Spitze geht es nicht mehr nach oben (Steigung ist nicht da). Die Steigung der Tangente an dieser Stelle ist eben 0. Deswegen die erste Ableitung gleich 0 setzen und die Gleichung lösen. Du erhältst ein, oder mehrere xE .
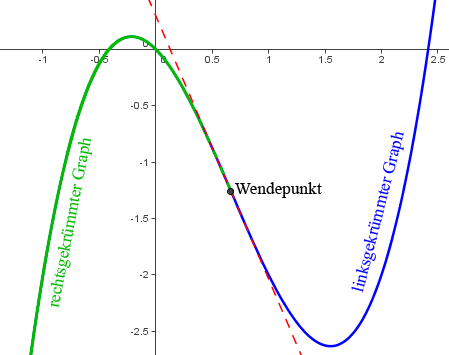
(iii) Hinreichende Bedingung: f''(xE) untersuchen
Hier setzt du die berechneten Stellen ein und untersuchst, ob dieser Wert größer, oder kleiner, als 0 ist.
Wenn f''(x)>0 => linksgekrümmt => x ist eine Minimalstelle
Wenn f''(x)<0 => rechtsgekrümmt => x ist eine Maximalstelle
Sattelpunkte sind per Definition keine Extrempunkte. Meistens hat man Sattelpunkte wenn f''(x)=0.
Dies macht man, um sich das Krümmungsverhalten des Graphen zu f anzuschauen, woraus man folgern kann, dass x eine Minimal-, oder eine Maximalstelle ist.
(iv) y-Koordinaten berechnen
Jetzt nur noch die berechneten Stellen von (ii) in die Funktionsgleichung einsetzen und die Funktionswerte berechnen. Anschließend noch die Punkte H und T, oder S aufschreiben.
Grüße und viel Erfolg beim Rechnen!